题目内容
7.如图①,△ABC是等边三角形,AB=AE,连接CE交AB于点H,(1)求证:∠BAE=2∠BCE;
(2)如图②,延长线AE,CB交于点F,点D在CB上,连接AD交CE于点G,当FA=FD时,求证:AH=BD;
(3)如图③,在(2)的条件下,把△ACD沿AD翻折,得到△AKD,K与C对应,AK交CE于点T,若CG=6,TG=4,求线段DG的长.
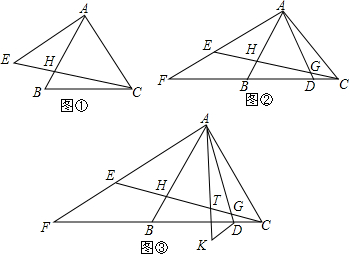
分析 (1)先判断∠E=∠ACE,再用等边三角形的性质计算求出结论;
(2)先判定∠FAB=2∠DAC,从而得到∠DAC=∠HCB.判断出△ACD≌△CBH,代换得到结论;
(3)作出辅助线,判断出△GKM为等边三角形,得到△TKG≌△DKM,即可.
解答 (1)证明:∵AE=AB,AB=AC,
∴AE=AC,
∴∠E=∠ACE.
∵△ABC是等边三角形,
∴∠BAC=∠B=∠ACB=60°,
∴∠ACE+∠BCE=60°,∠E+∠ACE+∠BAE=120°,
∴2∠ACE+∠BAE=120°,2(∠ACE+∠BCE)=120°,
∴∠BAE=2∠BCE.
(2)证明:∵FA=FD,
∴∠FAD=∠FDA=60°+∠DAC,
∴∠FAB+(60°-∠DAC)=60°+∠DAC,
∴∠FAB=2∠DAC.
∵∠FAB=2∠HCB,
∴∠DAC=∠HCB.
在△ACD和△CBH中,有
$\left\{\begin{array}{l}{∠DAC=∠HCB}\\{∠ACD=∠CBH=60°}\\{AC=CB}\end{array}\right.$,
∴△ACD≌△CBH(AAS),
∴BH=CD,
∵AB=BC,
∴AH=BD.
(3)如图③,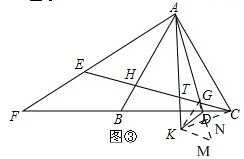
连接KC,GK,延长AD到M使GN=MN,
∴△GKM为等边三角形,
∴△TKG≌△DKM,
∴TG=DM=4,
∵GM=6,
∴GD=2,
点评 此题是几何变换综合题,主要考查了等边三角形的性质,等腰三角形的性质,全等三角形的判定和性质,构造等边三角形,解本题的关键判断△ACD≌△CBH和构造等边三角形.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5.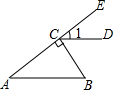 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
 如图,AE与CD交于点O,∠A=50°,OC=OE,∠C=25°,求证:AB∥CD.
如图,AE与CD交于点O,∠A=50°,OC=OE,∠C=25°,求证:AB∥CD.
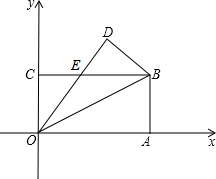 如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
如图,在平面直角坐标系中,长方形OABC的顶点A,C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.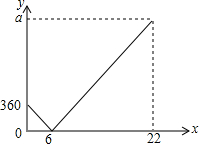 小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.
小明家、小芳家与人民公园依次在一条直线上,小明、小芳两人同时各自从家沿直线匀速步行到人民公园,已知小明到达公园花了22分钟,小芳的步行速度是40米/分钟,设两人出发x(分钟)后,小明离小芳家的距离为y(米),y与x的函数关系如图所示.