题目内容
11.已知关于x的方程4x2-(m+2)x=1-m有两个相等的实数根,求m的值和这个方程的根.分析 先把方程化为一般式,再根据判别式的意义得到△=(m+2)2-4×4×(m-1)=0,然后解方程求出m,再把m的值代入方程解关于x的方程即可.
解答 解:方程变形为4x2-(m+2)x+m-1=0,
△=(m+2)2-4×4×(m-1)=0,
整理得m2-12m+20=0,解得m1=2,m2=10,
当m=2时,方程为4x2-4x+1=0,解得x1=x2=$\frac{1}{2}$;
当m=10时,方程为4x2-12x+9=0,解得x1=x2=$\frac{3}{2}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
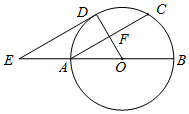 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.