题目内容
19．已知抛物线y=ax2+bx+c（a≠0）与x轴交于A、B两点，若点A的坐标为（-2，0），抛物线的对称轴为直线x=2，则线段AB的长为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 由抛物线的对称性可知点B的坐标（6，0），从而可求得AB的长．
解答 解：∵抛物线的对称轴为x=2，
∴点A与点B关于x=2对称．
∴点B的坐标为（6，0）．
∴AB=8．
故选：D．
点评 本题主要考查的是二次函数的图象和性质，根据抛物线的对称性求得点B的坐标是解题的关键．
练习册系列答案
相关题目
已知有理数a，b在数轴上如图所示，请你将a，-a，b，-b，0按从小到大的顺序排列-b＜a＜0＜-a＜b．
如图，△ABC中，AB=AC=6cm，∠BAC=120°，M、N分趴是AB，AC的中点，AD⊥BC，垂足为D，以D为圆心，3cm为半径画圆，判断A，B，C，M，N各点和⊙D的位置关系．
14．已知|x|=4，|y|=5，且xy＜0，则x+y的值等于（ ）
| A． | 9或-9 | B． | 9或-1 | C． | 1或-1 | D． | -9或-1 |
4．
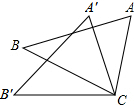如图，△ACB≌△A′CB，点A和点A′，点B和点B′是对应点，∠BCB′=30°，则∠ACA′的度数为（ ）
如图，△ACB≌△A′CB，点A和点A′，点B和点B′是对应点，∠BCB′=30°，则∠ACA′的度数为（ ）| A． | 20° | B． | 30° | C． | 35° | D． | 40° |
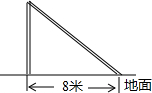如图，台风过后，一颗白杨树在高地某处断裂，白杨树的顶部落在离白杨树根部8米处，已知白杨树高16米，你能求出白杨树在离根部多少米的位置断裂吗？
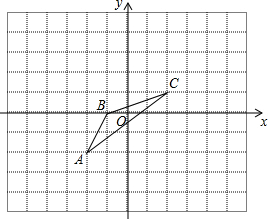如图，在平面直角坐标系中，
如图是小明制作的一个轴对称图形风筝，已知OC是对称轴，∠A=35°，∠BCO=30°，则∠AOC=115°．