题目内容
2.双曲线y=$\frac{6}{x}$上有三个点(-3,y1),(-1,y2),(2,y3),则y1,y2,y3的大小关系是y2<y1<y3.分析 根据反比例函数图象上点的坐标特征可计算出y1,y2,y3的值,然后比较它们的大小即可.
解答 解:∵点(-3,y1),(-1,y2),(2,y3)在双曲线y=$\frac{6}{x}$上,
∴y1=$\frac{6}{-3}$=-2,y2=$\frac{6}{-1}$=-6,y3=$\frac{6}{2}$=3,
∴y2<y1<y3.
故答案为y2<y1<y3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
相关题目
12.在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请判断下列结论:其中错误的结论是( )
| A. | BE=DF | B. | AG=GH=HC | C. | EG=$\frac{1}{2}$BG | D. | S△ABE=2S△AGE |
7.镇江市教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款60000元,已知“…”,设乙学校教师有x人,则可得方程$\frac{60000}{x}$-$\frac{60000}{(1+20%)x}$=20,根据此情景,题中用“…”表示的缺失的条件应补( )
| A. | 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| B. | 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% | |
| C. | 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| D. | 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% |
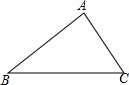 如图,三角形ABC中,∠BAC=70°,点D是射线BC上一点(不与点B、C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为70°或110°.
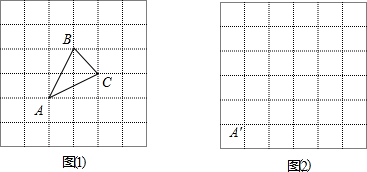
如图,三角形ABC中,∠BAC=70°,点D是射线BC上一点(不与点B、C重合),DE∥AB交直线AC于E,DF∥AC交直线AB于F,则∠FDE的度数为70°或110°.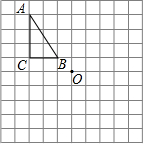 已知,如图△ABC,请在网格纸中画.
已知,如图△ABC,请在网格纸中画.