题目内容
15.已知A(-1,y1)、B(-2,y2)都在抛物线y=x2+1上,试比较y1与y2的大小:y1>y2.分析 先求得函数的对称轴为x=0,再判断A(-1,y1),B(-2,y2)在对称轴左侧,从而判断出y1与y2的大小关系.
解答 解:∵函数y=x2+1的对称轴为x=0,
∴A(-1,y1),B(-2,y2)在对称轴左侧,
∴抛物线开口向上,在对称轴左侧y随x的增大而减小.
∵-1<-2
∴y1>y2.
故答案为:>.
点评 此题考查了二次函数图象上点的特征,利用已知解析式得出对称轴进而利用二次函数增减性得出是解题关键.

练习册系列答案
相关题目
6.下列说法错误的是( )
| A. | 2x2-3xy-1是二次三项式 | B. | -x+1不是单项式 | ||
| C. | $-\frac{2}{3}πx{y^2}$的系数是$-\frac{2}{3}$ | D. | -22xab2的次数是4 |
3.等腰三角形的一边长等于4,另一边长等于10,则它的周长是( )
| A. | 18 | B. | 24 | C. | 18或24 | D. | 14 |
10.已知a-2b=3,则8-a+2b的值是( )
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |
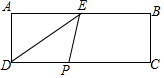 已知,如图,在长方形ABCD中,AB=8,AD=3,点E是AB的中点,点P是CD上的动点,点B关于直线PE的对称点为M,问:当CP的长为3或$\sqrt{7}$时,点M恰好落在△DEP的边上.
已知,如图,在长方形ABCD中,AB=8,AD=3,点E是AB的中点,点P是CD上的动点,点B关于直线PE的对称点为M,问:当CP的长为3或$\sqrt{7}$时,点M恰好落在△DEP的边上.