题目内容
11.计算:(1)|-3|+$\sqrt{9}$-(-1)2+(-$\frac{1}{2}$)0;
(2)(-3)0-|-$\sqrt{2}$|+$\sqrt{8}$;
(3)($\frac{1}{3}$)-2-(-1)2016-$\sqrt{25}$+(π-1)0.
分析 (1)原式利用绝对值的代数意义,算术平方根定义,乘方的意义,以及零指数幂法则计算即可得到结果;
(2)原式利用零指数幂法则,绝对值的代数意义,以及二次根式性质计算即可得到结果;
(3)原式利用零指数幂、负整数指数幂法则,乘方的意义,以及算术平方根定义计算即可得到结果.
解答 解:(1)原式=3+3-1+1=6;
(2)原式=1-$\sqrt{2}$+2$\sqrt{2}$=1+$\sqrt{2}$;
(3)原式=9-1-5+1=4.
点评 此题考查了实数的运算,零指数幂、负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.为了促进海峡两岸经济的发展,大陆相关部门干部原产台湾地区的15种水果实际进口零关税,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
销售单价从38元/千克下降了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)如果运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30元).若每天售价不低于30元/千克,一次进货最多只能是多少千克?
| 每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
| 每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)如果运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30元).若每天售价不低于30元/千克,一次进货最多只能是多少千克?
3.计算(-$\frac{1}{7}$)÷(-7)的结果为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{49}$ | D. | -$\frac{1}{49}$ |
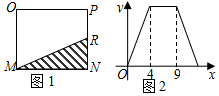 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,y的值为10.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,y的值为10.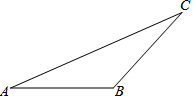 如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法)
如图,已知△ABC中,∠B>90°,请用尺规作出AB边的高线CD(请留作图痕迹,不写作法) 如图,已知点A、点B和直线l,在直线l上求作一点P,使PA=PB.(用直尺和圆规作图且保留作图痕迹)
如图,已知点A、点B和直线l,在直线l上求作一点P,使PA=PB.(用直尺和圆规作图且保留作图痕迹)