题目内容

1．化简并求值：（$\frac{a-2}{{{a^2}+2a}}$-$\frac{a-1}{{{a^2}+4a+4}}}$）÷$\frac{a-4}{a+2}$，其中a=-1．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．

解答 解：原式=[$\frac{a-2}{a（a+2）}$-$\frac{a-1}{（a+2）^{2}}$]•$\frac{a+2}{a-4}$=$\frac{a-2}{a（a-4）}$-$\frac{a-1}{（a+2）（a-4）}$=$\frac{（a-2）（a+2）-a（a-1）}{a（a+2）（a-4）}$=$\frac{a-4}{a（a+2）（a-4）}$=$\frac{1}{{{a^2}+2a}}$，
当a=-1时，原式=-1．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
1．某校八年级学生参加地理、生物学科中考模拟考试，现从中随机抽取了部分学生的地理考试成绩，进行统计后分为“优秀”、“良好”、“及格”、“不及格”四个等级，并将统计结果绘制成如下的统计图．请你结合图中所提供的信息，解答下列问题：

（说明：90分以上为优秀，89-75分为良好，74-60分为及格，60分以下为不及格．）
（1）请把条形统计图补充完整；
（2）扇形统计图中“不及格”等级所占的百分比是10%；
（3）扇形统计图中“优秀”等级所在的扇形的圆心角度数是72°；
（4）若该校初三共有950名学生，试估计该年级“优秀”和“良好”等级的学生共约为多少人．
12．小颖参加课外兴趣活动时设计了一个圆柱体模型，现有150张白纸，一张白纸可做侧面16个或底面43个，一个侧面与两个底面配成一套模型，则用多少张纸制底面，多少张纸制侧面，才能正好配成成套模型？
9．计算
（1）化简：$\frac{\sqrt{32}+\sqrt{50}}{\sqrt{2}}$-$\sqrt{18}$×$\sqrt{2}$，$\sqrt{\frac{2}{3}}$+$\sqrt{\frac{1}{6}}$-$\frac{1}{6}$$\sqrt{54}$  
（2）解方程组：$\left\{\begin{array}{l}{3m-2n=7}\\{m+2n=1}\end{array}\right.$，$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y-1}{3}=1}\\{x=2y}\end{array}\right.$．
16．（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=$\frac{1}{2}$∠ABC．以点B为旋转中心，将△BEC按逆时针方向旋转至△BEA（点C与点A重合，点E到点E处），连接DE．求证：DE'=DE．
（2）如图2，在△ABC中，BA=BC，∠ABC=90°，点D，E是AC边上的两点，且∠DBE=45°（即∠DBE=$\frac{1}{2}$∠ABC）．求证：DE2=AD2+EC2．
（3）如图3，在△ABC中，BA=BC，∠ABC=90°，点E是AC边上的点，点D是CA边延长线上的点，且∠DBE=45°．第（2）题中的结论：DE2=AD2+EC2还成立吗？如果成立，请给出证明；如果不成立，请说明理由．
6．下列说法正确的是（　　）
A．了解2017年报考飞行员的学生的视力情况应采取抽样调查
B．打开电视机，正在播放“神奇的动物去哪里”制作花絮是必然事件
C．为了初三1200名学生的体能状况，从中抽取了100名学生的成绩进行分析，1200是样本容量
D．7，9，9，4，9，8，8，这组数据的众数是9
13．如图，已知线段a，b，其中a＞b，求作直角三角形ABC，使得∠C为直角，AB=a，AC=b（尺规作图，保留作图痕迹，不写作法）
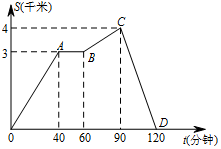10．为了提高身体素质，小明假期为自己制定了慢跑锻炼计划，某日小明从省体育场出发沿长安路慢跑，已知他离省体育场的距离s（ km）与时间t（h）之间的关系如图所示，根据图象回答下列问题：
（1）小明离开省体育场的最远距离是4千米，他在120分钟内共跑了8千米；
（2）小明在这次慢跑过程中，停留所用的时间为20分钟；
（3）小明在这段时间内慢跑的最快速度是每小时8千米．
11．计算：
（1）|-3|+$\sqrt{9}$-（-1）2+（-$\frac{1}{2}$）0；
（2）（-3）0-|-$\sqrt{2}$|+$\sqrt{8}$；
（3）（$\frac{1}{3}$）-2-（-1）2016-$\sqrt{25}$+（π-1）0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网