题目内容
方程x2-12x+y2+2=0的自然数解为 .
考点:非一次不定方程(组)
专题:
分析:先把方程化为(x-6)2+y2=34,要想找出自然数解,可把34分解为25和9,然后分别使(x-6)2=25,y2=9或(x-6)2=9,y2=25,求出自然数解.
解答:解:原方程可化为:(x-6)2+y2=34,
即(x-6)2+y2=25+9,
则可得:(x-6)2=25,y2=9或(x-6)2=9,y2=25,
当(x-6)2=25,y2=9时,
x-6=±5,y=±3,
则自然数解为:x=11或1,y=3;
当(x-6)2=9,y2=25时,
x-6=±3,y=±5,
则自然数解为:x=9或3,y=5.
故答案为:(11,3)或(1,3)或(9,5)或(3,5).
即(x-6)2+y2=25+9,
则可得:(x-6)2=25,y2=9或(x-6)2=9,y2=25,
当(x-6)2=25,y2=9时,
x-6=±5,y=±3,
则自然数解为:x=11或1,y=3;
当(x-6)2=9,y2=25时,
x-6=±3,y=±5,
则自然数解为:x=9或3,y=5.
故答案为:(11,3)或(1,3)或(9,5)或(3,5).
点评:本题考查了非一次不定方程,关键是把34分解为25和9,然后进行分类讨论,求出方程的自然数解,注意自然数为0和正整数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题错误的是( )
A、若 a<1,则(a-1)
| ||||||
B、若
| ||||||
| C、依次连接菱形各边中点得到的四边形是矩形 | ||||||
D、
|
下列说法中错误的是( )
| A、有限小数都是有理数 |
| B、无限小数都是无理数 |
| C、正数包括正有理数和正无理数 |
| D、负数包括负有理数和负无理数 |
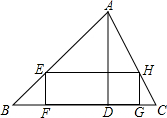 如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.
如图,一块三角形的铁皮,BC边为4厘米,BC边上的高AD为3厘米,要将它加工成一块矩形铁皮,使矩形的一边FG在BC上,其余两个顶点E,H分别在AB,AC上.设EF=x厘米,FG=y厘米.