题目内容
16．抛物线y=a（x-m）2+k（a＜0）经过点（0，5），（10，8），若0＜m＜10，则k的取值不可能是（ ）| A． | 8 | B． | 9 | C． | 10 | D． | 11 |
分析 根据解析式得出顶点坐标为（m，k）且经过点（0，5），（10，8），由于0＜m＜10，所以k的值不可能是5或8．
解答 解：由抛物线y=a（x-m）2+k（a＜0）可知：顶点坐标为（m，k），
∵抛物线y=a（x-m）2+k（a＜0）经过点（0，5），（10，8），
∴如果k=8时，则m=10，
∵0＜m＜10，
∴m≠10，则k≠8，
∴k的取值不可能是8，
故选A．
点评 本题考查了二次函数图象与系数的关系．二次函数的顶点坐标．
练习册系列答案
相关题目
4．如下表上边的表格给出了直线a上部分点（x，y）的坐标值，下边的表格给出了直线b上部分点（x，y）的坐标值，
（1）根据表格中的数据直接写出直线a和b的解析式；
（2）求出直线a和b的交点的坐标．
| x | -2 | 0 | 9 |
| y | -5 | -3 | 6 |
| x | -2 | 0 | 1.5 | 4 |
| y | 3 | 1 | -0.5 | -3 |
（2）求出直线a和b的交点的坐标．
11．在一个不透明的口袋中装有7个完全相同的小球，把它们分别标号为1，2，3，4，5，6，7，从中随机摸出一个小球，其标号大于3的概率为（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |
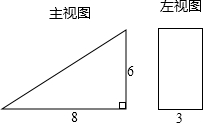有一个几何体的形状为直三棱柱，右图是它的主视图和左视图．