题目内容
4.如下表上边的表格给出了直线a上部分点(x,y)的坐标值,下边的表格给出了直线b上部分点(x,y)的坐标值,| x | -2 | 0 | 9 |
| y | -5 | -3 | 6 |
| x | -2 | 0 | 1.5 | 4 |
| y | 3 | 1 | -0.5 | -3 |
(2)求出直线a和b的交点的坐标.
分析 (1)先设直线的解析式为y=kx+b,再根据表(1)和表(2)分别求出k和b的值,从而得出直线a和直线b的解析式;
(2)根据直线a和直线b相交,得出$\left\{\begin{array}{l}{y=x-3}\\{y=-x+1}\end{array}\right.$,求出x,y的值,即可得出答案.
解答 解:(1)设直线a的解析式为y=kx+b,
根据表1可得:$\left\{\begin{array}{l}{-2k+b=-5}\\{b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
则直线a的解析式为y=x-3,
设直线b的解析式为y=kx+b,
根据表2可得:$\left\{\begin{array}{l}{b=1}\\{-2k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
则直线b的解析式为y=-x+1;
(2)∵直线a和直线b相交,
∴$\left\{\begin{array}{l}{y=x-3}\\{y=-x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,
∴直线a和b的交点的坐标是(2,-1).
点评 本题考查了待定系数法求一次函数解析式,联立两个函数的解析式求交点坐标是函数部分常用的方法,需熟练掌握并灵活运用.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
12.已知直线y=kx+b,若k+b<0,kb>0,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.在直角坐标系中,点P落在直线x-2y+6=0上,O为坐标原点,则|OP|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
9.正八边形的每个外角为( )
| A. | 60° | B. | 45° | C. | 35° | D. | 36° |
13.点A(cos30°,-sin30°)关于y轴对称的点的坐标是( )
| A. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) |
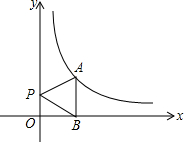 已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,
已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,