题目内容
15.解方程:$\sqrt{\sqrt{3}-\sqrt{\sqrt{3}+x}}$=x.分析 首先两边平方得出$\sqrt{3}$-x2=$\sqrt{\sqrt{3}+x}$,进一步两边平方整理后得出x4-2$\sqrt{3}$x2-x+3-$\sqrt{3}$=0,进一步分解因式探讨得出答案即可.
解答 解:$\sqrt{\sqrt{3}-\sqrt{\sqrt{3}+x}}$=x,
两边平方整理得$\sqrt{3}$-x2=$\sqrt{\sqrt{3}+x}$,
两边平方整理后得出x4-2$\sqrt{3}$x2-x+3-$\sqrt{3}$=0,
(x2-x-$\sqrt{3}$)(x2+x+1-$\sqrt{3}$)=0,
x2-x-$\sqrt{3}$=0,x2+x+1-$\sqrt{3}$=0,
(x-$\frac{1}{2}$)2=$\sqrt{3}$+$\frac{1}{4}$,(x+$\frac{1}{2}$)2=$\sqrt{3}$-$\frac{3}{4}$,
解得:x1=$\frac{\sqrt{4\sqrt{3}+1}+1}{2}$,x2=$\frac{-\sqrt{4\sqrt{3}+1}+1}{2}$,x3=$\frac{\sqrt{4\sqrt{3}-3}-1}{2}$,x4=$\frac{-\sqrt{4\sqrt{3}-3}-1}{2}$.
点评 此题考查二次根式的运用,一元二次方程的解法,掌握二次根式的性质和化简是解决问题的关键.

练习册系列答案
相关题目
10.计算2n+2•(-2)•(2n)2的结果为( )
| A. | -62n+1 | B. | -23n+2 | C. | -23n+3 | D. | -82n+3 |
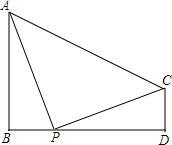 如图,已知AB丄BD,CD丄BD.
如图,已知AB丄BD,CD丄BD.
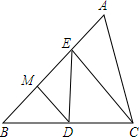 如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12.
如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12.