题目内容
11.在进行二次根式运算时,经常会遇到类似$\frac{3}{\sqrt{5}}$,$\frac{2}{\sqrt{3}+1}$的式子,其实我们还可以将其进一步变形:$\frac{3}{\sqrt{5}}$=$\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3}{5}$$\sqrt{5}$;$\frac{2}{\sqrt{3}+1}$=$\frac{2×(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{3}$-1.以上这种将分母变为有理式的恒等变形叫做分母有理化.
再如:$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$-$\sqrt{2}$
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\frac{\sqrt{5}-2}{(\sqrt{5})^{2}-(2)^{2}}$=$\sqrt{5}$-2
依照上述方法解答下列问题:
(1)填空:$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\sqrt{6}$-$\sqrt{5}$;$\frac{2}{\sqrt{7}-\sqrt{5}}$=$\sqrt{7}$-$\sqrt{5}$;$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$.
(2)化简求值:$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{289}+\sqrt{288}}$(写出解答过程)
分析 (1)利用材料中所给的方法求解即可;
(2)利用分母有理化的方法求解,注意消项.
解答 解:(1)$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\frac{\sqrt{6}-\sqrt{5}}{(\sqrt{6}+\sqrt{5})(\sqrt{6}-\sqrt{5})}$=$\frac{\sqrt{6}-\sqrt{5}}{(\sqrt{6})^{2}-(\sqrt{5})^{2}}$=$\sqrt{6}$-$\sqrt{5}$;
$\frac{2}{\sqrt{7}-\sqrt{5}}$=$\frac{2(\sqrt{7}+\sqrt{5})}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})}$=$\frac{2(\sqrt{7}+\sqrt{5})}{(\sqrt{7})^{2}-(\sqrt{5})^{2}}$=$\sqrt{7}$-$\sqrt{5}$;
$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n-1}-\sqrt{n})}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1})^{2}-(\sqrt{n})^{2}}$=$\sqrt{n+1}$-$\sqrt{n}$;
故答案是:$\sqrt{6}$-$\sqrt{5}$;$\sqrt{7}$-$\sqrt{5}$;$\sqrt{n+1}$-$\sqrt{n}$;
(2)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{289}+\sqrt{288}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{289}$-$\sqrt{288}$
=-1+$\sqrt{289}$
=-1+17
=16.
点评 本题主要考查了分母有理化,根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

| A. | ($\frac{5}{3}$a+b)元 | B. | (a+$\frac{5}{3}$b)元 | C. | $\frac{5}{3}$(a+b)元 | D. | (a+$\frac{5}{3}$b)元 |
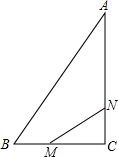 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,动点M以每秒1cm的速度从点B向点C移动;同时动点N以3cm的速度从点C向A移动,当点N到达点A时,两点都停止移动,连接MN,设移动时间为t秒.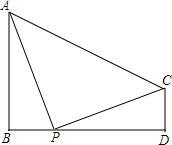 如图,已知AB丄BD,CD丄BD.
如图,已知AB丄BD,CD丄BD.