题目内容
17．分解因式：（1）3m4-48；
（2）b4-4ab3+4ab2．
分析 （1）原式提取公因式，再利用平方差公式分解即可；
（2）原式提取公因式，再利用完全平方公式分解即可．
解答 解：（1）原式=3（m4-16）=3（m2+4）（m+2）（m-2）；
（2）原式=b2（b2-4ab+4a）．
点评 此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
7．
如图，四边形PAOB是扇形OMN的内接矩形，顶点P在$\widehat{MN}$上，且不与M、N重合，当P点在$\widehat{MN}$上移动时，矩形PAOB的形状，大小随之变化，则AB的长度（ ）
如图，四边形PAOB是扇形OMN的内接矩形，顶点P在$\widehat{MN}$上，且不与M、N重合，当P点在$\widehat{MN}$上移动时，矩形PAOB的形状，大小随之变化，则AB的长度（ ）| A． | 不变 | B． | 变小 | C． | 变大 | D． | 不能确定 |
8．点M（-sin60°，cos60°）关于x轴对称的点的坐标是（ ）
| A． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$） | B． | （$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | C． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | D． | （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$） |
（1）请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题，判断这一逆命题是真命题还是假命题，如果是真命题给出证明，如果是假命题，说明理由．
已知：如图，△ABC中，BC=12，点O是BC上的一个动点，连结AO，点P也是AO上的一个动点，过点P作PD∥AB交BC于D，PE∥AC交BC于E．
9．若反比例函数y=$\frac{k+2}{x}$的图象位于第二、四象限内，则k的取值范围是（ ）
| A． | k＞-2 | B． | k＜0 | C． | k＞0 | D． | k＜-2 |
6．
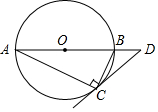如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作⊙O的切线，交AB的延长线于点D，则∠D的度数是（ ）
如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，∠A=25°，过点C作⊙O的切线，交AB的延长线于点D，则∠D的度数是（ ）| A． | 25° | B． | 30° | C． | 40° | D． | 55° |
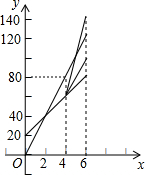某部队甲、乙现两班参加植树活动．乙班先植树20棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为y甲（棵），乙班植树的总量为y乙（棵），两班一起植树所用的时间（从甲班开始植树时计时）为x（时），y甲、y乙分别与x之间的部分函数图象如图所示．