题目内容
 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,写出图中两对相似三角形,并证明其中的一对.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G,写出图中两对相似三角形,并证明其中的一对.考点:相似三角形的判定
专题:
分析:根据三角形的外角性质求出∠AFM=∠BMG,再根据相似三角形的判定推出即可.
解答:答:△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM,
证明:∵∠DME=∠A=∠B,
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM.
证明:∵∠DME=∠A=∠B,
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM.
点评:本题考查了相似三角形的判定和三角形外角性质的应用,主要考查学生运用定理进行推理的能力,用到的知识点是有两角相等的两个三角形相似,难度适中.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
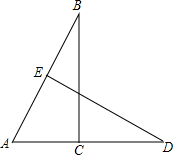 如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )
如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )| A、∠AED>∠BED |
| B、∠AED<∠BED |
| C、∠AED=∠BED |
| D、无法确定 |
矩形、菱形都具有的性质是( )
| A、对角线相等 |
| B、每一条对角线平分一组对角 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
估计
-1的值( )
| 11 |
| A、在2到3之间 |
| B、在3到4之间 |
| C、在4到5之间 |
| D、在5到6之间 |
在下列实数中,无理数的是( )
| A、π | ||
B、0.
| ||
C、-
| ||
D、
|
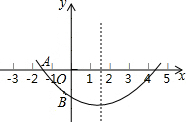 关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )
关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )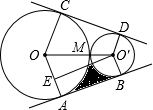 如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是
如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是 如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标.
如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标.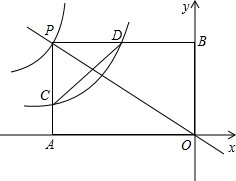 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=-