题目内容
 如图,为测量某广告牌面积,小明同学在广告牌正下方的观测点P的B,C,D的仰角分别为30°,45°,65°,若观测点P与广告牌右下角C的水平距离为6cm,你能根据以上数据求出广告牌的面积吗(结果取整数)?
如图,为测量某广告牌面积,小明同学在广告牌正下方的观测点P的B,C,D的仰角分别为30°,45°,65°,若观测点P与广告牌右下角C的水平距离为6cm,你能根据以上数据求出广告牌的面积吗(结果取整数)?考点:解直角三角形的应用-仰角俯角问题
专题:
分析:作BF垂直于地面于点F,作CE垂直于地面于点E,在直角△PCE中利用三角函数可求得CE的长,在直角△PDE中利用三角函数可求得DE的长,则CD的长可求得,在直角△BPF中利用三角函数可求得PF的长,则BC的长度即可求得,然后利用矩形的面积公式求解.
解答: 解:作BF垂直于地面于点F,作CE垂直于地面于点E,则PE=6cm.
解:作BF垂直于地面于点F,作CE垂直于地面于点E,则PE=6cm.
∵在直角△PCE中,tan∠CPE=
,
∴CE=PE•tan∠CPE=6×tan45°=6(cm).
同理,DE=PE•tan∠DPE=6tan65°≈6×2.145=12.87(cm)..
∴DC=DE-CE=12.87-6=6.87(cm).
∵在直角△BFP中,tan∠BPF=
,
∴PF=
=
=6
(cm).
则EF=PF+PE=6
+6=6(
+1)(cm).
则出广告牌的面积是:6(
+1)×6.87=41.22(1.732+1)=112.61304≈113(cm2).
答:广告牌的面积是113cm2.
 解:作BF垂直于地面于点F,作CE垂直于地面于点E,则PE=6cm.
解:作BF垂直于地面于点F,作CE垂直于地面于点E,则PE=6cm.∵在直角△PCE中,tan∠CPE=
| CE |
| PE |
∴CE=PE•tan∠CPE=6×tan45°=6(cm).
同理,DE=PE•tan∠DPE=6tan65°≈6×2.145=12.87(cm)..
∴DC=DE-CE=12.87-6=6.87(cm).
∵在直角△BFP中,tan∠BPF=
| BF |
| PF |
∴PF=
| BF |
| tan30° |
| CE |
| tan30° |
| 3 |
则EF=PF+PE=6
| 3 |
| 3 |
则出广告牌的面积是:6(
| 3 |
答:广告牌的面积是113cm2.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
在式子
、
、9x+
、
+
中,分式的个数有( )
| 1 |
| a |
| 3a2b3c |
| 4 |
| 10 |
| y |
| x |
| 7 |
| y |
| 8 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各组中的两个代数式,不是同类项的是( )
A、2x2y与-
| ||
| B、23与22 | ||
| C、a2b与-5ba2 | ||
| D、x2与32 |
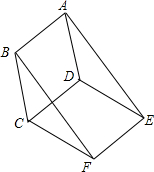 如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )
如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )| A、4个 | B、3个 | C、2个 | D、1个 |
矩形、菱形都具有的性质是( )
| A、对角线相等 |
| B、每一条对角线平分一组对角 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
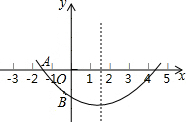 关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )
关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )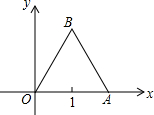 如图,已知等边三角形OAB的边长为2,求三个顶点的坐标.
如图,已知等边三角形OAB的边长为2,求三个顶点的坐标.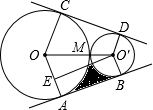 如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是
如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是