题目内容
10.已知实数a,b满足(a+1)2=1-2(a+1),2(b+1)=1-(b+1)2,且a≠b.求b$\sqrt{\frac{b}{a}}$+a$\sqrt{\frac{a}{b}}$的值.分析 首先把(a+1)2=1-2(a+1),2(b+1)=1-(b+1)2化为(a+1)2+2(a+1)-1=0,(b+1)2+2(b+1)-1=0,用根与系数的关系求出a+b=-4,ab=2,再把b$\sqrt{\frac{b}{a}}$+a$\sqrt{\frac{a}{b}}$变成$\frac{(a+b)^{2}-2ab}{\sqrt{ab}}$,然后把前面的关系式代入即可求出代数式的值.
解答 解:∵实数a,b满足(a+1)2=1-2(a+1),2(b+1)=1-(b+1)2,
∴实数a,b满足(a+1)2+2(a+1)-1=0,(b+1)2+2(b+1)-1=0,
∴实数(a+1)、(b+1)是方程x2+2x-1=0的两根.
由根与系数的关系可知a+1+b+1=-2,(a+1)(b+1)=-1,
∴a+b=-4,ab=2,
∴原式=$\frac{(a+b)^{2}-2ab}{\sqrt{ab}}$=$\frac{16-4}{\sqrt{2}}$=6$\sqrt{2}$.
点评 本题考查了根与系数的关系,二次根式的化简,解题的关键是不要直接求根,而是要利用根与系数的关系,代入求值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.当$\frac{|a|}{a}$+$\frac{b}{|b|}$=0时,a与b的关系是( )
| A. | a与b互为相反数 | B. | a=1,b=1 | C. | a与b异号 | D. | a=b=0 |
19.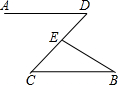 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
 如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )
如图,AD∥CB,∠D=43°,∠B=25°,则∠DEB的度数为( )| A. | 72° | B. | 68° | C. | 63° | D. | 18° |
 一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图)
一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图) 已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.
已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b. 胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)