题目内容
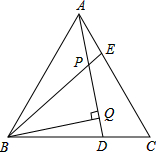 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.(1)求证:△ADC≌△BEA;
(2)若PQ=4,PE=1,求AD的长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质就可以得出AB=BC=AC,∠BAC=∠C=60°,就可以得出△ADC≌△BEA;
(2)由△ADC≌△BEA就可以得出∠DAC=∠EBA,AD=BE.既可以得出∠BPQ=60°,就可以求出PB的值,进而求出BE的值而得出结论
(2)由△ADC≌△BEA就可以得出∠DAC=∠EBA,AD=BE.既可以得出∠BPQ=60°,就可以求出PB的值,进而求出BE的值而得出结论
解答:解:(1)证明:∵△ABC是等边三角形,
∴AC=AB,∠C=∠BAE=60°,-
在△ADC与△BEA中,
,
∴△ADC≌△BEA(SAS);
(2)∵△ADC≌△BEA,
∴∠DAC=∠EBA,AD=BE.
∵∠BPQ=∠BAP+∠ABP,
∴∠BPQ=∠BAP+∠DAC=60°.
∵BQ⊥AD,
∴∠BQP=90°.
∴∠PBQ=30°
∴BP=2PQ.
∵PQ=4,
∴BP=8.
∵PE=1,
∴BE=BP+PE=9,
∴AD=BE=9.
答:AD=9.

∴AC=AB,∠C=∠BAE=60°,-
在△ADC与△BEA中,
|
∴△ADC≌△BEA(SAS);
(2)∵△ADC≌△BEA,
∴∠DAC=∠EBA,AD=BE.
∵∠BPQ=∠BAP+∠ABP,
∴∠BPQ=∠BAP+∠DAC=60°.
∵BQ⊥AD,
∴∠BQP=90°.
∴∠PBQ=30°
∴BP=2PQ.
∵PQ=4,
∴BP=8.
∵PE=1,
∴BE=BP+PE=9,
∴AD=BE=9.
答:AD=9.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列运算中,正确的是( )
| A、(a2)3=a5 |
| B、3a2÷2a=a |
| C、a2•a4=a6 |
| D、(2a)2=2a2 |
下列命题为真命题的是( )
| A、若两个图形沿某条直线对折后能够完全重合,那么这两个图形成轴对称 |
| B、有两边和一角分别相等的两个三角形全等 |
| C、直线y=2x-3在y轴上的截距为3 |
| D、△ABC中,若∠A=2∠B=3∠C,那么△ABC为直角三角形 |
 如图,在所给的网格图(每小格边长均为1的正方形)中,请完成下列各题:
如图,在所给的网格图(每小格边长均为1的正方形)中,请完成下列各题: