题目内容
3.某房间的地面由三种正多边形的地砖铺成,且每-个顶点处三种正多边形地砖各有一块,设这三种多边形地砖的边数分别是x、y、z,求$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$的值.分析 根据这三种正多边形一个顶点处三个内角的度数之和等于360°,得出$\frac{(x-2)×180°}{x}$+$\frac{(y-2)×180°}{y}$+$\frac{(z-2)×180°}{z}$=360°,再化简整理即可.
解答 解:设这三种多边形地砖的边数分别是x、y、z,
∵某房间的地面由三种正多边形的地砖铺成,且每-个顶点处三种正多边形地砖各有一块,
∴$\frac{(x-2)×180°}{x}$+$\frac{(y-2)×180°}{y}$+$\frac{(z-2)×180°}{z}$=360°,
∴1-$\frac{2}{x}$+1-$\frac{2}{y}$+1-$\frac{2}{z}$=2,
∴$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=$\frac{1}{2}$.
点评 此题主要考查了平面镶嵌,解决本题的关键是理解多个多边形镶嵌的条件是:一个顶点处的内角和等于一个周角.

练习册系列答案
相关题目
14.下列方程一定有实数根的是( )
| A. | x2+1=0 | B. | (2x+1)2+3=0 | C. | (x-1)2=0 | D. | ($\frac{1}{2}$x-a)2=a |
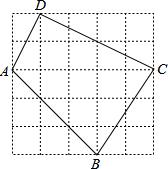 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形. △ABC中,AB=AC,AF⊥BC于点F,AD平分∠CAF,∠ADC=30°,BC=8,S△BCD=18,求BD的长.
△ABC中,AB=AC,AF⊥BC于点F,AD平分∠CAF,∠ADC=30°,BC=8,S△BCD=18,求BD的长.