题目内容
如图,已知在四边形ABCD中,AB=20cm,BC=15 cm,CD=7 cm,AD=24 cm,∠ABC=90°。猜想∠A与∠C关系并加以证明.
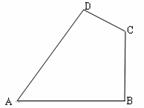

180°
【解析】
试题分析:连接AC.首先根据勾股定理求得AC的长,再根据勾股定理的逆定理求得∠D=90°,进而求出∠A+∠C=180°.
试题解析:∠A+∠C=180°
证明如下:
如图,连接AC.


∵AB=20cm,BC=15cm,∠ABC=90°,
∴由勾股定理,得
AC2=AB2+BC2=625(cm2).
又∵在△ADC中,CD=7cm,AD=24cm,
∴CD2+AD2=AC2,
∴∠D=90°.
∴∠A+∠C=360°-180°=180°.
【难度】较易

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 中,函数值
中,函数值 随
随 的增大而 .
的增大而 . 部分折成一个无盖的长方体盒子.
部分折成一个无盖的长方体盒子.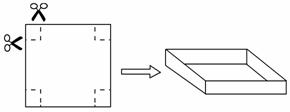


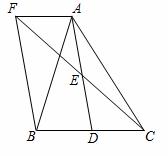



 .
. ,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .
,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为 .