题目内容
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
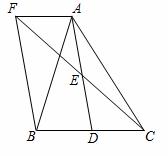

(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
(1)∵AF∥BC,∴∠EAF=∠EDC,∵E是AD的中点,∴AE=DE,在△EAF和△EDC中,∵∠EAF=∠EDC,AE=DE,∠AEF=∠DEC,∴△EAF≌△EDC(ASA),∴DC=AF,又∵AF=BD,∴BD=DC,∴D是BC的中点;
(2)矩形,理由是:
∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形
∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∴四边形AFBD是矩形.
【解析】
试题分析:(1)利用△AEF≌△DEC来证;
(2)利用一组对边平行且相等的四边形是平行四边形,得出四边形AFBD是平行四边形,进而得出四边形AFBD是矩形.
试题解析:(1)∵AF∥BC,∴∠EAF=∠EDC,∵E是AD的中点,∴AE=DE,在△EAF和△EDC中,∵∠EAF=∠EDC,AE=DE,∠AEF=∠DEC,∴△EAF≌△EDC(ASA),∴DC=AF,又∵AF=BD,∴BD=DC,∴D是BC的中点;
(2)四边形AFBD是矩形.理由是:
∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形
∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∴四边形AFBD是矩形.
【难度】一般

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
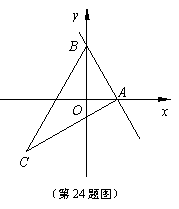 已知:如
已知:如 图,直线y=kx+2与x轴的正半轴相交于点A(t,0)、与y轴相交于点B,抛物线
图,直线y=kx+2与x轴的正半轴相交于点A(t,0)、与y轴相交于点B,抛物线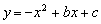 经过点A和点B,点C在第三象限内,且AC⊥AB,tan∠ACB=
经过点A和点B,点C在第三象限内,且AC⊥AB,tan∠ACB=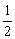 .
. 普通列车距离A站还有135km.求快车和普通列车的速度各是多少?
普通列车距离A站还有135km.求快车和普通列车的速度各是多少?




 ABCD中,点E、F在BD上,且BF=DE.
ABCD中,点E、F在BD上,且BF=DE.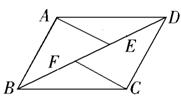

 .
. 等于 .
等于 .