题目内容
19．已知直角三角形的两条边长恰好是方程x2-7x+10=0的两个根，则此直角三角形的斜边长是5或$\sqrt{29}$．分析 利用分解因式法解一元二次方程可得出三角形的两条边长，当其中一边长为斜边长时，则此直角三角形的斜边长为方程较大的根；当两边均为直角边长时，利用勾股定理可求出此直角三角形的斜边长．此题得解．
解答 解：∵x2-7x+10=（x-2）（x-5）=0，
解得：x1=2，x2=5．
当方程的一根为斜边长时，此直角三角形的斜边长为5；
当方程的两根为直角边长时，此直角三角形的斜边长为$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$．
故答案为：5或$\sqrt{29}$．
点评 本题考查了分解因式法解一元二次方程以及勾股定理，分方程两根有斜边长与方程两根均为直角边长两种情况考虑是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．下列运算正确的是（ ）
| A． | m3•m3=2m3 | B． | 5m2n-4mn2=mn | C． | （m+1）（m-1）=m2-1 | D． | （m-n）2=m2-mn+n2 |
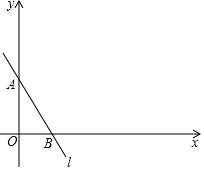如图，已知一次函数y=-$\frac{4}{3}$x+4的图象是直线l，设直线l分别与y轴、x轴交于点A、B．
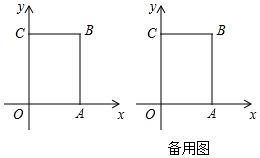如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a，b满足|a-4|+$\sqrt{b-6}$=0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动．
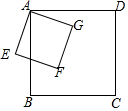如图，正方形ABCD的边长为2cm，正方形AEFG的边长为1cm，正方形AEFG绕点A旋转的过程中，线段CF的长的最小值为$\sqrt{2}$cm．