题目内容
6. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DA平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB;⑤A、D两点一定在线段EC的垂直平分线上,其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由条件可证明△ACD≌△AED,从而可判断①、④正确;利用直角三角形的两锐角互余可判断②;利用角平分线的定义可判断③;利用线段垂直平分线的判定可判断⑤;从而可得出答案.
解答 解:
∵DE⊥AB,
∴∠C=∠DEA=90°,
∵AD平分∠BAC,
∴CD=DE,
在Rt△ACD和Rt△AED中
$\left\{\begin{array}{l}{CD=DE}\\{AD=AD}\end{array}\right.$
∴Rt△ACD≌Rt△AED(HL),
∴∠EDA=∠CDA,
∴DA平分∠CDE,AC=AE
故①正确;
∵AB=AE+BE,且AC=AE,
∴AC+BE=AB;
故④正确;
∵AE=AB,DE=DC,
∴A、D都在线段CD的垂直平分线上,
∴AD是线段CE的垂直平分线,
故⑤正确;
∵∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠BDE,
故②正确;
若DE平分∠ADB,则E应为AB中点,由条件无法得出,
故③不正确;
综上可知正确的结论有:①②④⑤,共四个,
故选C.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
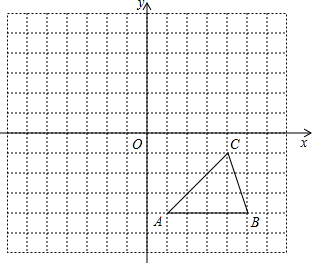 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1)
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1) 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△AED对折至△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②FG=FC;③AG∥CF;④S△FGC=$\frac{18}{5}$,其中正确结论是①③④(填序号).
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△AED对折至△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②FG=FC;③AG∥CF;④S△FGC=$\frac{18}{5}$,其中正确结论是①③④(填序号). 问题情境:一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶端滑下0.4米,那么梯子的底部向外滑出多远?
问题情境:一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶端滑下0.4米,那么梯子的底部向外滑出多远? 如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?
如图,墙A处需要维修,A处距离墙脚C处8米,墙下是一条宽BC为6米的小河,现要架一架梯子维修A处的墙体,现有一架12米长的梯子,问这架梯子能否到达墙的A处?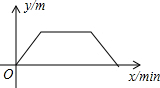 如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )
如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )