题目内容
12.计算(1)$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$
(2)$({\sqrt{6}+\sqrt{2}})({\sqrt{6}-\sqrt{2}})$
(3)$({\sqrt{3}+1})({\sqrt{3}-1})-\sqrt{{{({-3})}^2}}+{({\sqrt{2}-1})^0}+\frac{1}{{\sqrt{2}-1}}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式计算;
(3)利用平方差公式、零指数幂和分母有理化得到原式=3-1-3+1+$\sqrt{2}$+1,然后合并即可.
解答 解:(1)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(2)原式=6-2
=4;
(3)原式=3-1-3+1+$\sqrt{2}$+1
=$\sqrt{2}$+1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.下列运算中,正确的是( )
| A. | 3a2-a2=2 | B. | (-a2b)3=a6b3 | C. | a3•a6=a9 | D. | (2a2)2=2a4 |
1.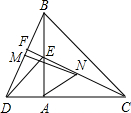 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点A,D,C在同一直线上,直线CE交BD于F,连接AF,点M,N分别是BD,CE的中点,有下列说法:①BD=CE;②CF⊥BD;③AF平分∠DFC;④△AMN是等腰直角三角形.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.下列命题错误的是( )
| A. | 对角线相互平分的四边形是平行四边形 | |
| B. | 对角线相互平分且相等的四边形是矩形 | |
| C. | 对角线相互平分且垂直的四边形是菱形 | |
| D. | 对角线相等且垂直的四边形是正方形 |
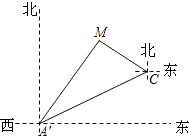 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,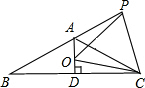 已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,