题目内容
3.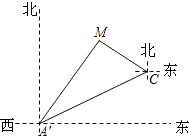 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,(1)∠MAC=30°,∠MCA=60°;
(2)请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求MN的长.
分析 (1)作MT∥AB,根据平行线的性质及方向角的定义得出∠5=∠2=30°,∠TMC=∠1=60°,那么∠AMC=30°+60°=90°.在Rt△ACM中,根据方向角的定义及角的和差得出∠3=∠BAC-∠2=30°,即∠MAC=30°,再由直角三角形两锐角互余求出∠MCA=60°;
(2)过M作MN⊥AC交于N点,即MN最短,先解Rt△ACM,求出CM=$\frac{1}{2}$AC=1000米,再解Rt△NCM,求出CN=$\frac{1}{2}$CM=500米,MN=$\sqrt{3}$CN=500$\sqrt{3}$米.
解答  解:(1)作MT∥AB.
解:(1)作MT∥AB.
根据题意,得∠2=30°,∠BAC=60°,AC=2000米,∠1=60°.
∵MT∥AB,
∴∠5=∠2=30°,∠TMC=∠1=60°,
∴∠AMC=30°+60°=90°.
在Rt△ACM中,∵∠3=∠BAC-∠2=60°-30°=30°,
即∠MAC=30°,
∴∠MCA=90°-∠3=60°;
(2)过M作MN⊥AC,垂足为N,此时MN最小.
在Rt△ACM中,∵∠3=30°,
∴CM=$\frac{1}{2}$AC=1000米,
在Rt△NCM中,∵∠CMN=30°,
∴CN=$\frac{1}{2}$CM=500米,MN=$\sqrt{3}$CN=500$\sqrt{3}$米.
故答案为30°,60°.
点评 此题考查了解直角三角形的应用-方向角问题,其中涉及到平行线的性质,方向角的定义,直角三角形的性质,垂线段最短的性质,含30度角的直角三角形三边的关系等知识,难度不大.正确作出高线,证明△AMC是直角三角形是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.在下列乘法运算中,不能用乘法公式计算的是( )
| A. | 78×82 | B. | (x-y)(-y+x) | C. | (2x+y)(4x-y) | D. | (a-b+c)(a-b-c) |
18.在平面直角坐标系中,点P(3,-x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.在下列各对数值中,是方程2x+3y=-6的解的一组数值是( )
| A. | $\left\{\begin{array}{l}x=0\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=-3\\ y=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$ |
 如图,在平移三角尺画平行线的过程中,理由是同位角相等,两直线平行.
如图,在平移三角尺画平行线的过程中,理由是同位角相等,两直线平行.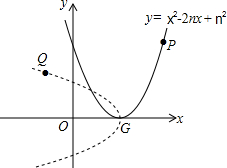 如图,已知抛物线y=x2-2nx+n2(n为常数,n>0),它的顶点为G,点P为抛物线右侧上任一点(不与G重合).
如图,已知抛物线y=x2-2nx+n2(n为常数,n>0),它的顶点为G,点P为抛物线右侧上任一点(不与G重合).