题目内容
使等式成立
(1)x2+2x+ =(x+ )2
(2)x2-6x+ =(x- )2
(3)4x2+4x+ =(2x+ )2
(4)x2+3x+ =(x+ )2
(5)x2-
x+ =(x- )2
(6)x2+
x+ =(x- )2.
(1)x2+2x+
(2)x2-6x+
(3)4x2+4x+
(4)x2+3x+
(5)x2-
| 7 |
| 2 |
(6)x2+
| b |
| a |
考点:配方法的应用
专题:
分析:常数项是一次项系数一半的平方.注意(4)中,把2x2看作一个整体.
解答:解:常数项是一次项系数一半的平方.
(1)x2+2x+1=(x+1)2
(2)x2-6x+9=(x-3)2
(3)4x2+4x+1=(2x+1)2
(4)x2+3x+
=(x+
)2
(5)x2-
x+
=(x-
)2
(6)x2+
x+
=(x-
)2.
故答案是:(1)1;1;
(2)9;3;
(3)1;1;
(4)
;
;
(5)
;
;
(6)
;
.
(1)x2+2x+1=(x+1)2
(2)x2-6x+9=(x-3)2
(3)4x2+4x+1=(2x+1)2
(4)x2+3x+
| 9 |
| 4 |
| 3 |
| 2 |
(5)x2-
| 7 |
| 2 |
| 49 |
| 4 |
| 7 |
| 4 |
(6)x2+
| b |
| a |
| b2 |
| 4a2 |
| b |
| 2a |
故答案是:(1)1;1;
(2)9;3;
(3)1;1;
(4)
| 9 |
| 4 |
| 3 |
| 2 |
(5)
| 49 |
| 16 |
| 7 |
| 4 |
(6)
| b2 |
| 4a2 |
| b |
| 2a |
点评:此题考查了学生的应用能力,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.
利用配方法求二次三项式是一个完全平方式时所含字母系数的值.关键是二次三项式是完全平方式,则常数项是一次项系数一半的平方.
利用配方法求二次三项式是一个完全平方式时所含字母系数的值.关键是二次三项式是完全平方式,则常数项是一次项系数一半的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若关于x的一元二次方程ax2+bx+c=0(a≠0)中有a-b+c=0,则该方程中必有一根是( )
| A、0 | B、1 | C、-1 | D、±1 |
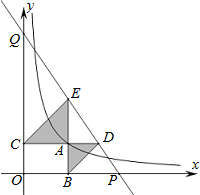 如图,已知动点A在函数
如图,已知动点A在函数