题目内容
6.若直角三角形的两直角边长分别为5、12,则它的内切圆的半径为( )| A. | 6 | B. | 2.5 | C. | 2 | D. | 4 |
分析 用勾股定理求出斜边AC的长,连接OD,OE,OF,根据切线的性质得出四边形OFBD是正方形,根据正方形的性质得到四条边相等,设出圆的半径为r,根据切线长定理得到AD=AE=12-r,同理可得出CE=CF=5-r,进而得到AC=AE+EC=AD+CF,列出关于r的方程,求出方程的解可得出r的值.
解答 解:如图所示: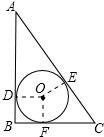
∵直角三角形的两直角边长BC=5,AC=12,
∴根据勾股定理得:直角三角形的斜边AC=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
又圆O为三角形的内切圆,D,E,F分别为切点,连接OD,OE,OF,
∴OD⊥AB,OF⊥BC,
∴∠ODB=∠B=∠OFB=90°,
∴四边形OFBD为矩形,又OD=OF,
∴四边形OFBD为正方形,
∴OD=DB=BF=OF,
又AD,AE为圆O的两条切线,
∴AD=AE,
同理CE=CF,BD=BF,
设圆O的半径为r,则有BD=BF=r,
∴CF=CE=5-r,AD=AE=12-r,
又AC=AE+EC=AD+CF=12-r+5-r=17-2r=13,
解得:r=2,
则该直角三角形的内切圆的半径为2.
故选:C.
点评 此题考查了三角形的内切圆与内心、勾股定理,正方形的判定与性质、切线长定理;利用了方程及转化的思想,本题的关键是根据题意画出相应的图形,添加合适的辅助线,设出未知数,建立方程来解决问题.

练习册系列答案
相关题目
16.某地要把248吨物资从某地运往甲、乙两地,用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围).
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 运往地车型 | 甲地(元/辆) | 乙地(元/辆) |
| 大货车 | 620 | 700 |
| 小货车 | 400 | 550 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围).
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
17.下面所给的交通标志是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
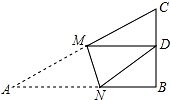 如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为$\frac{8}{3}$.
如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为$\frac{8}{3}$.