Question

如图1，平面直角坐标系中，抛物线y=ax²+bx+c与x轴交于A、B两点，与y轴交于点C，顶点为M．D在y轴上，OB=OD=3，OA=5．

（1）试用含a的式子表示点M的坐标；

（2）若S_△ABC﹣S_△ACM=；

①求抛物线y=ax²+bx+c的解析式；

②如图2，将△BOD绕点O沿逆时针方向旋转α（0°＜α≤180°）得到△B′OD′，直线AD与BC相交于点Q，求点Q纵坐标的取值范围．

　

Answer 1

【考点】二次函数综合题．

【分析】（1）由线段长度，确定点A，B坐标代入y=ax²+bx+c即可用a表示抛物线，运用顶点公式即可求出点M坐标；

（2）①用a表示△ABC与△ACM的面积，根据题意列方程求解即可；

②根据题意分析出：以点O为圆心，以OB为半径作圆，当AD与圆O在第二象限内相切时，Q的纵坐标最大，当AD与圆O在第三象限内相切时，Q的纵坐标最小，

分别求解即可，求解时，先确定切点坐标，求出两条直线解析式，联立直线解方程组求出y的值即可．

【解答】解：（1）由OB=OD=3，OA=5可得，

点A（﹣5，0），B（3，0），D（0，5），

设抛物线的解析式为y=a（x﹣3）×（x+5），

整理得：y=ax²+2ax﹣15a，

所以顶点M（﹣1，﹣16a）；

（2）如图1

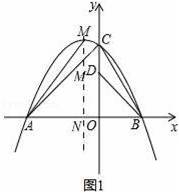
过点M作MN⊥x轴，垂足为N，交直线AC于点H，

y=ax²+2ax﹣15a，令x=0，解得：y=﹣15a，

所以：C（0，﹣15a）

设直线AC解析式为：y=mx+n，

由A（﹣5，0），C（0，﹣15a），坐标可得，，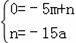

解得：，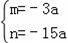

所以直线AC：y=﹣3ax﹣15a，

由M（﹣1，﹣16a），可得，

点H（﹣1，﹣12a），

所以MH=﹣16a﹣（﹣12a）=﹣4a，

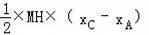
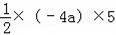
所以：S_△ACM===﹣10a，

S_△ABC=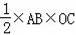=﹣60a，

由S_△ABC﹣S_△ACM=，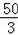

解得：a=﹣，

所以：抛物线的解析式为：y=；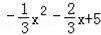

②如图2

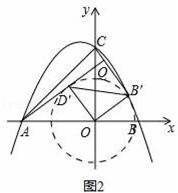
以点O为圆心，以OB为半径作圆，当AD与圆O在第二象限内相切时，Q的纵坐标最大，

此时，易求点D′的坐标为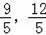（﹣），点A（﹣5，0）；点B′（），

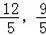
用两点法可求直线AD′解析式为：y=，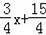

直线B′C的解析式为：，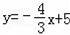

联立，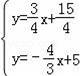

解得y=，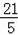

如图3

以点O为圆心，以OB为半径作圆，当AD与圆O在第三象限内相切时，Q的纵坐标最小，

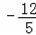
此时易求点D′（，），点A（﹣5，0）；点B′（﹣），

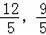
用两点法可求直线AD′解析式为：，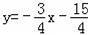

直线B′C的解析式为：，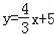

联立，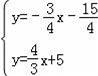

解得：y=．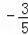

所以：点Q纵坐标的取值范围为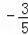：≤y≤．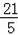

【点评】此题主要考查二次函数的综合问题，会用已知点求解析式，会根据点的坐标表示三角形面积，会运用圆的知识分析解决旋转的相关问题是解题的关键．