Question

如图，已知抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，O是坐标原点，点A的坐标是（﹣1，0），点C的坐标是（0，﹣3）

（1）求抛物线的函数表达式；

（2）求直线BC的函数表达式；

（3）P为线段BC上一点，连接AC，AP，若∠ACB=∠PAB，求△PAB的面积．

Answer 1

【考点】二次函数综合题．

【分析】（1）根据待定系数法，可得函数解析式；

（2）根据自变量与函数值的对应关系，可得B点坐标，根据待定系数法，可得函数解析式；

（3）根据两个角对应相等的两个三角形相似，相思三角形的性质，可得BP的长，再根据平行线截三角形所得的三角形相似，相似三角形的性质，可得BD的长，根据三角形的面积公式，可得答案．

【解答】解：（1）将A、C点坐标代入函数解析式，得

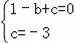
，解得，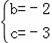

抛物线的解析式为y=x²﹣2x﹣3；

（2）当y=0时，x²﹣2x﹣3=0，解得x=﹣1（不符合题意，舍），x=3，即B点坐标为（3，0）．

设直线BC的解析式为y=kx+b，将B、C点的坐标代入，得

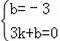
，解得，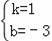

直线BC的解析式为y=x﹣3；

（3）如图，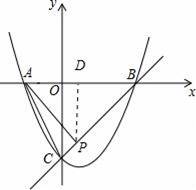

过点P作PD⊥x轴于点D，∵∠ACB=∠PAB，∠ABC=∠PBA，

∴△ABP∽△CBA， =．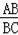

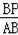
∵BO=OC=3，

∴BC=3．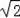

∵A（﹣1，0），B（3，0），

∴AB=4，∴ =，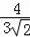

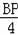
解得BP=．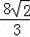

由题意可得：PD∥OC，

∴△BDP∽△BOC，∴ ==，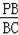

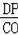
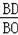
则==，

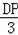
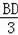
解得DP=BD=，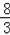

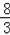
S_△APB=AB•PD=××4=．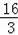

【点评】本题考查了二次函数综合题，利用待定系数法求函数解析式；利用相似三角形的判定与性质得出PD的长是解题关键．