题目内容
如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面成60°角，在离电线杆6米的B处安置测角仪，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果保留根号）．
【考点】解直角三角形的应用-仰角俯角问题．
【分析】作AG⊥CD，垂足为G．在Rt△AGC中，根据CG=AG•tan30°，求出CG的长；在Rt△CED中，根据CE=
，求出CE的长．
【解答】解：作AG⊥CD，垂足为G．
易得AG=BD，
在Rt△AGC中，CG=AG•tan30°=6×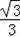
=2
米，
可得CD=CG+GD=（2+1.5）米，
在Rt△CED中，CE=
=
=（4+）米．
答：拉线CE的长为（4+）米．
【点评】本题考查了解直角三角形﹣﹣仰角俯角问题，熟悉三角函数和解直角三角形的应用是解题的关键．
练习册系列答案
相关题目
经过点C(2，3)，直线y＝kx＋b与抛物线相交于A、B两点，∠ACB＝90°
，
)，直接写出直线AB的解析式 ；取点B(4，﹣3)，直接写出AB的解析式为 
；
．