题目内容
10.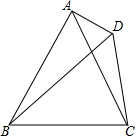 如图,△ABC是等边三角形,D是△ABC外一点,且∠BDC=60°,判断DA、DB、DC的数量关系.
如图,△ABC是等边三角形,D是△ABC外一点,且∠BDC=60°,判断DA、DB、DC的数量关系.
分析 结论:BD=DA+DC.在DM上截取一点M,使得DM=DC,只要证明△CAD≌△CBM即可解决问题.
解答 解:结论:BD=DA+DC.
理由:如图,在DM上截取一点M,使得DM=DC.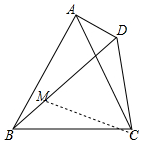
∵∠BDC=60°,
∴△DMC是等边三角形,∵△ABC是等边三角形,
∴DC=CM=DM,∠DCM=∠ACB=60°,CA=CB,
∴∠ACD=∠BCM,
在△CAD和△CBM中,
$\left\{\begin{array}{l}{CD=CM}\\{∠ACD=∠BCM}\\{CA=CB}\end{array}\right.$,
∴△CAD≌△CBM,
∴BM=AD,
∴BD=BM+DM=AD+DC.
点评 本题考查了全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.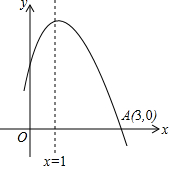 如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )
 如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④4a+2b+c<0.其中错误的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.二次函数y=ax2+bx+c(a≠0)对于x的任何值都恒为负值的条件是( )
| A. | a>0,?△>0 | B. | a>0,?△<0 | C. | a<0,?△>0 | D. | a<0,?△<0 |
5.下列方程中是关于x的一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | (x-1)(x+2)=1 | C. | ax2+bx+c=0 | D. | x2-2x-3 |
2.在下列各数-$\frac{22}{7}$,0,1.5,-3,5$\frac{1}{2}$,50%,+8中,是整数的有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
19.下列各数在数轴上的位置是在-2的左边的是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |