题目内容
4.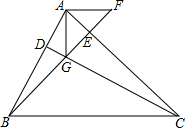 如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.
如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,且AB=CG,AC=BF.(1)求证:△ABF≌△GCA;
(2)求证:AG⊥AF.
分析 (1)根据垂直定义得出∠BDC=∠GEC=90°,根据等角的余角相等求出∠ABF=∠ACG,根据全等三角形的判定推出即可;
(2)根据全等三角形的性质得出∠F=∠GAC,求出∠GAC+∠FAE=90°,即可得出答案.
解答 证明:(1)∵CD⊥AB,BE⊥AC,
∴∠BDC=∠GEC=90°,
∵∠DGB=∠EGC,
∴∠ABF=∠ACG(等角的余角相等),
在△ABF和△GCA中,
$\left\{\begin{array}{l}{AB=CG}\\{∠ABF=∠ACG}\\{BF=AC}\end{array}\right.$,
∴△ABF≌△GCA;
(2)由(1)△ABF≌△GCA,
∴∠F=∠GAC,
∵BE⊥AC,
∴∠AEB=∠F+∠FAE=90°,
∴∠GAC+∠FAE=90°,
∴AG⊥AF.
点评 本题考查了全等三角形的性质和判定,垂直定义的应用,能求出△ABF≌△GCA是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
12.先填表,再回答问题:
(1)当x为何值时,代数式2x-1的值等于5?
(2)已知有两个x的值使代数式-3x和x2的值相等,你能找出这两个x值吗?
(3)随着x的值的逐渐增大,代数式2x-1、-3x和x2的值是如何变化的?(写出结论即可,无需说明理由)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x-1 | |||||||
| -3x | |||||||
| x2 |
(2)已知有两个x的值使代数式-3x和x2的值相等,你能找出这两个x值吗?
(3)随着x的值的逐渐增大,代数式2x-1、-3x和x2的值是如何变化的?(写出结论即可,无需说明理由)
19.正方体的截面中,边数最多的多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
9.若$\sqrt{\frac{x-1}{x+2}}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x<-2 | C. | 1≤x<-2 | D. | x≥1或x<-2 |
16.下列说法其中正确的个数有( )
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.与数轴上的点一一对应的数是( )
| A. | 分数 | B. | 有理数 | C. | 无理数 | D. | 实数 |
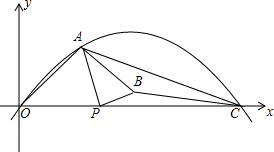 如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC.
如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC. 如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.
如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.