题目内容
 如图,以两条直线l1,l2的交点坐标为解的方程组是
如图,以两条直线l1,l2的交点坐标为解的方程组是考点:一次函数与二元一次方程(组)
专题:
分析:两条直线的交点坐标应该是联立两个一次函数解析式所组成的方程组的解.因此本题需先根据两直线经过的点的坐标,用待定系数法求出两直线的解析式.然后联立两函数的解析式可得出所求的方程组.
解答:解:设一次函数的解析式为:y=kx+b(k≠0).
①∵直线l1经过(3,0)、(0,-3),
∴
,
解得,
,
∴函数l1解析式为y=x-3,即x-y=3;
②∵直线l2经过(-2,0)、(0,-1),
∴
,
解得,
,
∴函数l2解析式为y=-
x-1,即
x+y=-1;
因此以两条直线l1,l2的交点坐标为解的方程组是:
.
故答案是:
.
①∵直线l1经过(3,0)、(0,-3),
∴
|
解得,
|
∴函数l1解析式为y=x-3,即x-y=3;
②∵直线l2经过(-2,0)、(0,-1),
∴
|
解得,
|
∴函数l2解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
因此以两条直线l1,l2的交点坐标为解的方程组是:
|
故答案是:
|
点评:本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
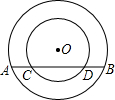 如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,设大圆和小圆的半径分别为a、b,求证:AD•BD=a2-b2.
如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,设大圆和小圆的半径分别为a、b,求证:AD•BD=a2-b2. 某公司共有50名员工,据初步统计,原来每人每年用于购买饮用瓶装矿泉水的支出约200元,经测算和市场调查,若该公司集体改饮“加林山”牌桶装矿泉水,则年费用由两部分组成:一部分是购买纯净水费用,另一部分为电费及购置饮水机等费用共约800元,其中矿泉水的销售价y与年购买总量x之间的关系如图所示:
某公司共有50名员工,据初步统计,原来每人每年用于购买饮用瓶装矿泉水的支出约200元,经测算和市场调查,若该公司集体改饮“加林山”牌桶装矿泉水,则年费用由两部分组成:一部分是购买纯净水费用,另一部分为电费及购置饮水机等费用共约800元,其中矿泉水的销售价y与年购买总量x之间的关系如图所示: