题目内容
已知,点A在y轴的正半轴上,点B在x轴的负半轴上,过A作CA⊥AB于A,且AB=AC.
(1)若A(0,4),B(-1,0),求C的坐标;
(2)点D在x轴的负半轴上且OA=OD,连接DC交y轴的正半轴于E,求
.
(1)若A(0,4),B(-1,0),求C的坐标;
(2)点D在x轴的负半轴上且OA=OD,连接DC交y轴的正半轴于E,求
| OE |
| BD |
考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)求点C的坐标关键是找到点C到x轴、y轴的距离.所以只需过点C作y轴的垂线段后通过三角形全等求出点C到x轴、y轴的距离即可.
(2)运用全等三角形的判定和性质发现AO=DO,AF=BO,OE=FE,从而可发现BD=2OE.
(2)运用全等三角形的判定和性质发现AO=DO,AF=BO,OE=FE,从而可发现BD=2OE.
解答:解:(1)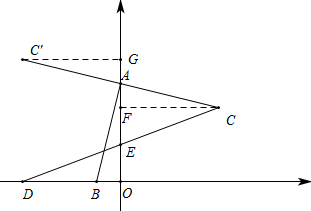
如图,当点C在第一象限时,过点C作CF⊥OA,垂足为F
∴∠CFA=∠AOB=90°
∴∠CAF+∠BAO=90°,∠BAO+∠ABO=90°
∴∠CAF=∠ABO
在△ACF和△BAO中
∴△ACF≌△BAO(AAS)
∴CF=AO=4,AF=BO=1
∴C(4,3)
当点C在第二象限时,同理可求C(-4,5)
(2)C点有两个位置C或C',当C点在第一象限时,才有交点E,
当B点在D点位置时,C点正好在x轴上,
因为DC交y轴的正半轴于E,所以B点在OD线段上,
作CF垂直于AO于点F,
根据AAS得到△ABO≌△ACF,
∴CF=AO,AF=BO,
∵AO=DO,
∴CF=DO,
在△CEF和△DEO中,
,
∴△CEF≌△DEO(AAS),
∴EF=EO,
∵AO=DO,AF=BO,
∴BD=OF=2OE,
∴
=
.

如图,当点C在第一象限时,过点C作CF⊥OA,垂足为F
∴∠CFA=∠AOB=90°
∴∠CAF+∠BAO=90°,∠BAO+∠ABO=90°
∴∠CAF=∠ABO
在△ACF和△BAO中
|
∴△ACF≌△BAO(AAS)
∴CF=AO=4,AF=BO=1
∴C(4,3)
当点C在第二象限时,同理可求C(-4,5)
(2)C点有两个位置C或C',当C点在第一象限时,才有交点E,
当B点在D点位置时,C点正好在x轴上,
因为DC交y轴的正半轴于E,所以B点在OD线段上,
作CF垂直于AO于点F,
根据AAS得到△ABO≌△ACF,
∴CF=AO,AF=BO,
∵AO=DO,
∴CF=DO,
在△CEF和△DEO中,
|
∴△CEF≌△DEO(AAS),
∴EF=EO,
∵AO=DO,AF=BO,
∴BD=OF=2OE,
∴
| OE |
| BD |
| 1 |
| 2 |
点评:本题主要考查了学生全等三角形的判定和性质的综合运用以及如何求平面直角坐标系中点的坐标.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,已知线段AD,B为AC的中点,M为AD中点,CD=
如图,已知线段AD,B为AC的中点,M为AD中点,CD=| 2 |
| 3 |
| A、MC=AC-MD | ||
B、AM=
| ||
C、BC=
| ||
D、AB=
|
 如图,A,B,C,D是⊙O上的四个点,点A是
如图,A,B,C,D是⊙O上的四个点,点A是
 如图,以两条直线l1,l2的交点坐标为解的方程组是
如图,以两条直线l1,l2的交点坐标为解的方程组是