Question

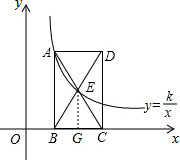已知如图：点（1，3）在函数y=

k

x

（x＞0）的图象上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=

k

x

（x＞0）的图象又经过A、E两点，点E的横坐标为m，解答下列问题：
（1）求k的值；
（2）求点A的坐标；（用含m代数式表示）
（3）当∠ABD=45°时，求m的值．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）把（1，3）代入反比例函数解析式即可；
（2）BG=CG，求出OB即可，A在反比例函数解析式上，求出AB，即A的纵坐标，代入反比例函数解析式即可求出A的横坐标；
（3）∠ABD=45°时，AB=BD，把（2）中的代数式代入即可求解．

解答： 解：（1）由函数y=

k

x

图象过点（1，3），
则把点（1，3）坐标代入y=

k

x

中，
得：k=3，y=

3

x

；
（2）连接AC，则AC过E，过E作EG⊥BC交BC于G点
∵点E的横坐标为m，E在双曲线y=

k

x

上，
∴E的纵坐标是y=

3

m

，
∵E为BD中点，
∴由平行四边形性质得出E为AC中点，
∴BG=GC=

1

2

BC，
∴AB=2EG=

6

m

，
即A点的纵坐标是

6

m

，
代入双曲线y=

3

x

得：A的横坐标是

1

2

m，
∴A（

1

2

m，

6

m

）；
（3）当∠ABD=45°时，AB=AD，
则有

6

m

=m，即m²=6，
解得：m₁=

6

，m₂=-

6

（舍去），
∴m=

6

．

点评：本题考查了反比例函数的综合知识；若函数过某个点，这个点的坐标应适合这个函数解析式；另外，平行于x轴的直线上的点的纵坐标相等；培养学生综合运用知识的能力和探究精神．