题目内容
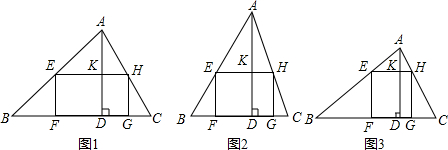
如图,在锐角△ABC中,AD是BC边上的高线,矩形EFGH的顶点E,H分别在AB,AC上,F,G在BC边上,AD与EH相交于点K.
(1)如图1,若BC=10,AD=5,EH=2EF,求EF,EH的长.
(2)如图2,若BC=AD=8,求矩形EFGH的周长.
(3)如图3,若四边形EFGH是边长为4的正方形,且S△AEH:S△HGC:S△BEF=1:1:3,求△ABC的面积.
(1)如图1,若BC=10,AD=5,EH=2EF,求EF,EH的长.
(2)如图2,若BC=AD=8,求矩形EFGH的周长.
(3)如图3,若四边形EFGH是边长为4的正方形,且S△AEH:S△HGC:S△BEF=1:1:3,求△ABC的面积.

考点:相似三角形的判定与性质
专题:
分析:(1)根据相似三角形对应边比例相等性质即可解题;
(2)根据相似三角形对应边比例相等性质可解;
(3)根据相似三角形对应边比值相等可以求得AK的值,即可求△ABC的面积.
(2)根据相似三角形对应边比例相等性质可解;
(3)根据相似三角形对应边比值相等可以求得AK的值,即可求△ABC的面积.
解答:解:(1)∵矩形EFGH,
∴EH∥BC,AK=AD-KD=AK-EF,
∴
=
=
,
∵EH=2EF,
∴AK=EF=
,EH=2EF=5;
(2)∵
=
,
=
,
∴
=
=
,
∴
=1-
,
∴
+
=1,
∵AD=BC
∴EF+FG=AD=8,
∴矩形EFGH的周长为16.
(3)设AK=x,
∵S△AEH:S△HGC:S△BEF=1:1:3,
∴AK:GC:BF=1:1:3,
∵
=
,
∴
=
,
解得x=2,
∴△ABC的面积为
BC•AD=
×12×6=36.
∴EH∥BC,AK=AD-KD=AK-EF,
∴
| AK |
| AD |
| EH |
| BC |
| AD-EF |
| AD |
∵EH=2EF,
∴AK=EF=
| 5 |
| 2 |
(2)∵
| EF |
| AD |
| BF |
| BD |
| GH |
| AD |
| CG |
| CD |
∴
| BF |
| BD |
| CG |
| CD |
| EF |
| AD |
∴
| FG |
| BC |
| BF+CG |
| BC |
∴
| EF |
| AD |
| FG |
| BC |
∵AD=BC
∴EF+FG=AD=8,
∴矩形EFGH的周长为16.
(3)设AK=x,
∵S△AEH:S△HGC:S△BEF=1:1:3,
∴AK:GC:BF=1:1:3,
∵
| AK |
| AD |
| EH |
| BC |
∴
| x |
| x+4 |
| 4 |
| 3x+x+4 |
解得x=2,
∴△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了相似三角形对应边比值相等的性质,考查了三角形面积的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x=-3时,代数式3-2x的值是( )
| A、-3 | B、9 | C、1 | D、0 |
化简(a-b)-(a+b)的结果是( )
| A、-2b | B、a-2b |
| C、0 | D、3a |
将圆周率π精确到千分位,应是( )
| A、3.14 |
| B、3.141 |
| C、3.1415 |
| D、3.142 |
边长为2的正方形的面积是4,边长为3的正方形的面积是9,则面积是6的正方形的边长a满足( )
| A、a是整数 |
| B、2<a<3 |
| C、2<a<3,且a为分数 |
| D、a不存在 |
 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB. 已知:如图,D,E分别在△ABC的边BC,AC上,AD,BE交于点G,AD⊥BC,点F在AD上,且△EFG∽△BDG.
已知:如图,D,E分别在△ABC的边BC,AC上,AD,BE交于点G,AD⊥BC,点F在AD上,且△EFG∽△BDG.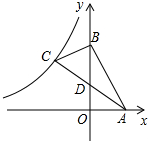 如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且
如图,直线y=-2x+6与坐标轴相交于点A、点B,BC⊥AB,且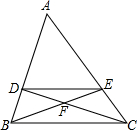 如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=
如图,已知DE∥BC,且BF:EF=4:3,则AE:EC=