题目内容
19.等腰三角形ABC中,AB=AC,AD⊥BC于点D,点E在直线AC上,2CE=AC,AD=6,BE=5,则△ABC的面积是16或$\frac{18}{5}$.分析 根据等腰三角形三线合一的性质可得到AD是底边BC的中线,从而得到点G为△ABC的重心,从而不难求得DG,BG的长,再根据勾股定理求得BD的长,最后根据三角形面积公式求解即可.
解答 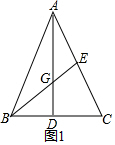 解:如图1,∵在等腰△ABC中,AB=AC,AD⊥BC于D,
解:如图1,∵在等腰△ABC中,AB=AC,AD⊥BC于D,
∴AD是底边BC的中线,
∵2CE=AC,
∴G为△ABC的重心,
∵AD=6,BE=5,
∴DG=$\frac{1}{3}$AD=2,BG=$\frac{2}{3}$BE=3$\frac{1}{3}$,
∴在直角△BDG中,由勾股定理得到:BD=$\sqrt{B{G}^{2}-D{G}^{2}}$=$\frac{8}{3}$,BC=2BD=$\frac{16}{3}$,
∴S△ABC=$\frac{1}{2}$BC×AD=16.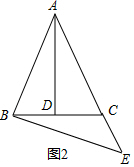 如图2,∵在等腰△ABC中,AB=AC,AD⊥BC于D,
如图2,∵在等腰△ABC中,AB=AC,AD⊥BC于D,
∴AD是底边BC的中线,
∵2CE=AC,
∴G为△ABC的重心,
∵AD=6,BE=5,
∴DG=$\frac{1}{3}$AD=2,BG=$\frac{2}{3}$BE=3$\frac{1}{3}$,
∴在直角△BDG中,由勾股定理得到:BD=$\sqrt{B{G}^{2}-D{G}^{2}}$=$\frac{8}{3}$,BC=2BD=$\frac{16}{3}$,
∴S△ABC=$\frac{1}{2}$BC×AD=16.
故答案为:16或$\frac{18}{5}$.
点评 此题主要考查等腰三角形的性质及勾股定理的综合运用.本题的难点是得到BC的长.

练习册系列答案
相关题目
10. 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )| A. | a>-2 | B. | a<-3 | C. | -a<b | D. | a<-b |
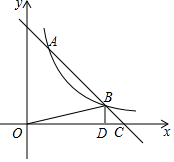 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴交于点C,过点B作BD⊥x轴于点D,△BDC的面积是$\frac{1}{2}$,则k的值为( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴交于点C,过点B作BD⊥x轴于点D,△BDC的面积是$\frac{1}{2}$,则k的值为( )