题目内容
5．
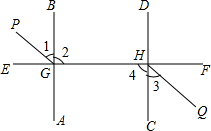如图，AB⊥EF于G，CD⊥EF于H，GP平分∠EGB，HQ平分∠CHF，试找出图中有哪些平行线？并说明理由．
分析 根据垂直可得∠2=∠EGB=90°，∠4=∠CHF=90°，再根据内错角相等，两直线平行可得AB∥CD；再根据角平分线的性质可得∠1=45°，∠3=45°，然后可得∠1+∠2=∠3+∠4=135°，再根据内错角相等，两直线平行可得GP∥HQ．
解答 解：AB∥CD，GP∥HQ，
理由：∵AB⊥EF于点G，CD⊥EF于点H，
∴∠2=∠EGB=90°，∠4=∠CHF=90°，
∴AB∥CD（内错角相等，两直线平行）．
∵GP平分∠EGB，HQ平分∠CHF，
∴∠1=45°，∠3=45°，
∴∠1+∠2=∠3+∠4=135°，
∴PG∥HQ（内错角相等，两直线平行）．
点评 本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
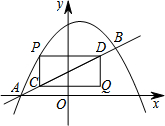如图，抛物线$y=-\frac{1}{2}{x^2}+bx+c$与直线$y=\frac{1}{2}x+1$交于A、B两点，点A在x轴上，点B的横坐标是2．点P在直线AB上方的抛物线上，过点P分别作PC∥y轴、PD∥x轴，与直线AB交于点C、D，以PC、PD为边作矩形PCQD，设点Q的坐标为（m，n）．
如图所示，AB=DC，AD=BC，DE=BF，求证：BE=DF．