题目内容
1.如图,在Rt△ACB中,∠ACB=90°,AC=3,BC=6,D为BC上一点,CD=2,射线DG,BC交AB于点G.点P从点A出发以每秒$\sqrt{5}$个单位长度的速度沿AB方向运动,点Q从点D出发以每秒2个单位长度的速度沿射线DG运动,P、Q两点同时出发,当点P到达点B时停止运动,点Q也随之停止,过点P作PE⊥AC于点E,PF⊥BC于点F,得到矩形PECF,点M为点D关于点Q的对称点,以QM为直角边,在射线DG的右侧作Rt△QMN,使QN=2QM.设运动时间为t(单位:秒).(1)当点N恰好落在PF上时,求t的值.
(2)当△QMN和矩形PECF有重叠部分时,直接写出重叠部分图形面积S与t的函数关系式以及自变量t的取值范围.
(3)连接PN、ND、PD,是否存在这样的t值,使△PND为直角三角形?若存在,求出相应的t值若不存在,请说明理由.
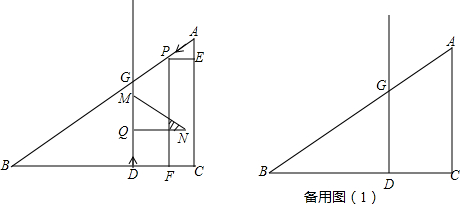
分析 (1)由勾股定理求得AB=3$\sqrt{5}$,根据题意可得QN=2QM=4t,再由△APE∽△ABC表示出AE的长度,根据QN=CD-PE,建立方程求得t的值;
(2)首先应明确各节点重叠图形的变化,根据重叠图形的形状表示重叠部分图形面积S与t的函数关系式,也可得出相应自变量t的取值范围;
(3)分别表示出PN、ND、PD,分三种情况讨论,再由勾股定理,可得t的值.
解答 解:(1)∵∠ACB=90°,AC=3,BC=6,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3$\sqrt{5}$,
∵△APE∽△ABC,
∴$\frac{AP}{AB}$=$\frac{PE}{BC}$,
即$\frac{\sqrt{5}t}{3\sqrt{5}}$=$\frac{PE}{6}$,
∴PE=2t,FC=PE=2t,DF=3-2t,
∵点N恰好落在PF上,QN=2QM=4t,
∴2t=3-4t,
解得:t=$\frac{1}{3}$.
(2)①当$\frac{1}{3}$<t≤$\frac{2}{3}$时,如图所示: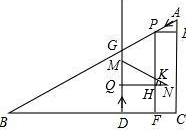
HN=4t-(2-2t)=6t-2,KH=$\frac{1}{2}$HN=3t-1,
∴S=$\frac{1}{2}$(6t-2)(3t-1)=9t2-6t+1;
②$\frac{2}{3}$≤t<$\frac{4}{5}$时,S=5t2-2t;
③当$\frac{4}{5}$≤t<1时,S=-31t2+46t-16;
④当1≤t<$\frac{3}{2}$时,S=-6t2+6t.
(3)DN2=DQ2+QN2=(2t)2+(4t)2=20t2,
PD2=DF2+PF2=(2-2t)2+(3-t)2=5t2-14t+13,
PN2=HN2+PH2=[4t-(2-2t)]2+(3-t-2t)2=45t2-42t+13,
①当∠PND=90°时,20t2+45t2-42t+13=5t2-14t+13,
解得:t1=0(舍去),t2=$\frac{7}{15}$;
②当∠PDN=90°时,20t2+(5t2-14t+13)=45t2-42t+13,
解得:t1=0(舍去),t2=$\frac{7}{5}$,
③当∠PDN=90°时,(5t2-14t+13)+(45t2-42t+13)=20t2,
解得:t1=1,t2=$\frac{13}{15}$,
综上可得:t=$\frac{7}{15}$或$\frac{7}{5}$或1或$\frac{13}{15}$.
点评 此题考查了相似三角形的综合题,相似三角形的性质,分类讨论利用勾股定理解决问题,利用三角形的面积重叠图形的形状得出S与t的关系式,注意数形结合思想的运用.

 阅读快车系列答案
阅读快车系列答案| A. | x=$\frac{4}{3}$ | B. | x=$\frac{4}{5}$ | C. | x=$\frac{2}{3}$ | D. | x=$\frac{5}{4}$ |
| A. | 3.7×10-5克 | B. | 3.7×10-6克 | C. | 3.7×10-7克 | D. | 3.7×10-8克 |
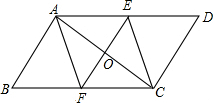 如图,E、F分别是?ABCD的边AD、BC的中点,EF和AC相交于O,则AC、EF互相平分,说明你的理由.
如图,E、F分别是?ABCD的边AD、BC的中点,EF和AC相交于O,则AC、EF互相平分,说明你的理由.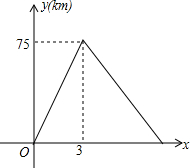 在松花江沿岸依次有A、B、C旅游景点,一观光游船由A景点顺流出发经过B景点到达C景点后立即返回,A、B两个景点之间的距离为25km,当游船到达B景点时恰好由一艘橡皮艇从B景点漂流而下,游船离开A景点的距离y(km)与其行驶时间x(h)之间的函数关系如图所示.
在松花江沿岸依次有A、B、C旅游景点,一观光游船由A景点顺流出发经过B景点到达C景点后立即返回,A、B两个景点之间的距离为25km,当游船到达B景点时恰好由一艘橡皮艇从B景点漂流而下,游船离开A景点的距离y(km)与其行驶时间x(h)之间的函数关系如图所示.