Question

4．如图所示，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动，若如果P、Q同时出发：
（1）几秒钟后，可使CP=CQ？
（2）几秒钟后，可使PQ长为3$\sqrt{5}$cm？
（3）几秒钟后，可使四边形APQB的面积占△ABC的面积三分之二？
（4）若点P从点A出发沿边AC-CB方向移动，点Q从C点出发沿CB-BA方向移动，是否存在某一时刻，使得△PBQ为等腰三角形？

Answer 1

分析 （1）根据题意用t表示出CP、CQ，根据题意列出方程，解方程即可；
（2）根据勾股定理列出算式，计算即可；
（3）根据三角形的面积公式列式计算；
（4）分QB=QP的两种情况、BP=BQ根据等腰三角形的性质计算即可．

解答 解：（1）设t秒钟后，CP=CQ，
由题意得，CP=6-t，CQ=2t，
则6-t=2t，
解得，t=2，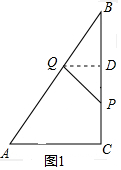
则2秒钟后，CP=CQ；
（2）由题意得，（6-t）²+（2t）²=（3$\sqrt{5}$）²，
解得，t₁=3，t₂=-$\frac{3}{5}$（舍去），
答：3秒钟后，PQ长为3$\sqrt{5}$cm；
（3）△ABC的面积为：$\frac{1}{2}$×6×8=24cm²，
∵四边形APQB的面积占△ABC的面积三分之二，
∴△ACP的面积占△ABC的面积三分之一，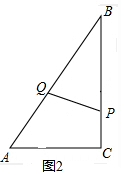
∴$\frac{1}{2}$×（6-t）×2t=$\frac{1}{3}$×24，
解得，t₁=2，t₂=4，
答：2秒或4秒钟后，可使四边形APQB的面积占△ABC的面积三分之二；
（4）当QB=QP时，$\sqrt{（6-t）^{2}+（2t）^{2}}$=8-2t，
解得，t₁=-8$\sqrt{2}$-10（舍去），t₂=8$\sqrt{2}$-10，
如图1，当QB=QP时，作QD⊥BC于D，
则$\frac{BQ}{BA}$=$\frac{BD}{BC}$，即$\frac{2t-8}{10}$=$\frac{\frac{8-t}{2}}{8}$，
解得，t=$\frac{104}{21}$，
当BP=BQ时，如图2：
14-t=2t-8，
解得，t=$\frac{22}{3}$，
综上所述，当t=8$\sqrt{2}$-10或$\frac{104}{21}$或$\frac{22}{3}$时，△PBQ为等腰三角形．

点评 本题考查的是三角形知识的综合运用，掌握等腰三角形的判定和性质、灵活运用分情况讨论思想是解题的关键．