题目内容

12．解方程组：
（1）$\left\{\begin{array}{l}{x+y=5}\\{x-y=-3}\end{array}\right.$                    
（2）$\left\{\begin{array}{l}\frac{x}{3}-\frac{y}{2}=1\\ 3y=-2（x+1）\end{array}\right.$．

分析 （1）方程组利用加减消元法求出解即可；
（2）方程组整理后，利用加减消元法求出解即可．

解答 解：（1）$\left\{\begin{array}{l}{x+y=5①}\\{x-y=-3②}\end{array}\right.$，
①+②得：2x=2，即x=1，
把x=1代入①得：y=4，
则方程组的解为$\left\{\begin{array}{l}x=1\\ y=4\end{array}\right.$；
（2）方程组整理得：$\left\{\begin{array}{l}{2x-3y=6①}\\{2x+3y=-2②}\end{array}\right.$，
①+②得：4x=4，即x=1，
②-①得：6y=-8，即y=-$\frac{4}{3}$，
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-\frac{4}{3}}\end{array}\right.$．

点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

练习册系列答案
相关题目
2．如图，已知AB是⊙O的直径，点E是弧BC的中点，DE与BC交于点F，∠CEA=∠ODB．
（1）请判断直线BD与⊙O的位置关系，并说明理由；
（2）当AB=12，BF=3$\sqrt{3}$时，求图中阴影部分的面积．
3．阅读以下计算过程：
计算：|-7$\frac{3}{8}$+4$\frac{1}{2}$|-|-18$\frac{1}{4}$|+|-6-$\frac{1}{2}$|．
解：原式=：-7$\frac{3}{8}$+4$\frac{1}{2}$-18$\frac{1}{4}$|+6+$\frac{1}{2}$
=（-7+6+4-18）+（$\frac{1}{2}$+$\frac{1}{2}$）+（-$\frac{3}{8}$-$\frac{1}{4}$）
=-15+1-$\frac{5}{8}$
=-14$\frac{5}{8}$．
回答：
（1）上述解答过程是否有错误？
（2）错误的理由是什么？
（3）把第二步的解法用一句话概括出来应是什么？
20．已知关于x的一元二次方程x2+（2m-1）x+m2=0有两个实数根x1和x2．
（1）求实数m的取值范围；
（2）当x1x2-2x1-2x2=10时，求m的值．
7．将下列各数在数轴上表示出来，并将他们用“＞”连接起来
-$\frac{1}{2}$，|-2.5|，0，（-2）2，-（+2）
17．如图，长方形OABC的边OA在x轴正半轴上，边OC在y轴正半轴上，B点的坐标为（1，3）．长方形O'A'BC'是长方形OABC绕B点逆时针旋转得到的．O'点恰好在x轴的正半轴上，O'C'交AB于点D．
（1）求证：O'A=O'A'，并求点O'的坐标．（提示：连接BO、BO'）
（2）求边C'O'所在直线的解析式．
（3）延长BA到M使AM=1，在（2）中求得的直线上是否存在点P，使得△POM是以线段OM为直角边的直角三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．
4．如图所示，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动，若如果P、Q同时出发：
（1）几秒钟后，可使CP=CQ？
（2）几秒钟后，可使PQ长为3$\sqrt{5}$cm？
（3）几秒钟后，可使四边形APQB的面积占△ABC的面积三分之二？
（4）若点P从点A出发沿边AC-CB方向移动，点Q从C点出发沿CB-BA方向移动，是否存在某一时刻，使得△PBQ为等腰三角形？
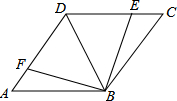1．如图，BD是菱形ABCD的对角线，点E，F分别在边CD，DA上，且CE=AF．求证：DE=DF．
2．用简便方法计算：
（1）99$\frac{71}{72}$×（-36）
（2）（-48）×0.125+48×$\frac{1}{8}$+（-48）×$\frac{5}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网