题目内容
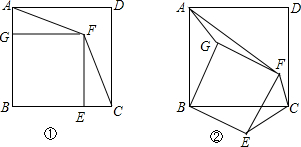
10.如图①,E是正方形ABCD内的边BC上的一点,以BC为边在ABCD内作正方形BEFG,连接AF、FC.小亮发现在图①中,下面三个结论成立:
(1)AF=FC;
(2)AG=CE;
(3)AG⊥CE;
现在将正方形BEFG按顺时针旋转一个角度α,得到图②,你猜测在图②中上述结论哪些仍然成立?说明理由.
分析 由旋转的性质得∠ABG=∠CBE=α,根据四边形ABCD,BEFG是正方形,于是得到AB=BC,BG=BE,通过ABG≌△BCE,得到AG=CE;延长AB,CE交于M,过点B作BN∥AG交CM于N,根据平行线的性质得到∠BAN=∠MBN,由∠BAN=∠BCM,推出△MNB∽△MBC,得到∠MNB=∠MBC=90°于是得到结论.
解答 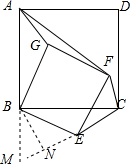 解:(1)AF=FC不成立;(2)AG=CE成立;(3)AG⊥CE成立;
解:(1)AF=FC不成立;(2)AG=CE成立;(3)AG⊥CE成立;
证明:由旋转的性质得∠ABG=∠CBE=α,
∵四边形ABCD,BEFG是正方形,
∴AB=BC,BG=BE,
在△ABG与△CBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABG=∠EBC}\\{BG=BE}\end{array}\right.$,
∴△ABG≌△BCE,
∴AG=CE;故(2)成立;
延长AB,CE交于M,过点B作BN∥AG交CM于N,
∴∠BAN=∠MBN,
∵△ABG≌△BCE,
∴∠BAN=∠BCM,
∴∠MBN=∠BCM,
∵∠M=∠M,
∴△MNB∽△MBC,
∴∠MNB=∠MBC=90°,
∴BN⊥MC,
∴AG⊥EC.
故成立.
点评 本题考查了正方形的性质,全等三角形的判定和性质.相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
 一次函数y=ax+b在直角坐标系中的图象如图所示,则a-b<0(填>,<或=)
一次函数y=ax+b在直角坐标系中的图象如图所示,则a-b<0(填>,<或=)