题目内容
11.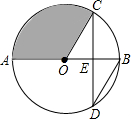 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积为( )| A. | π | B. | 4π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
分析 首先证明OE=$\frac{1}{2}$OC=$\frac{1}{2}$OB,则可以证得△OEC≌△BED,则S阴影=半圆-S扇形OCB,利用扇形的面积公式即可求解.
解答 解:连结BC.
∵∠COB=2∠CDB=60°,
又∵OB=OC,∴△OBC是等边三角形.
∵E为OB的中点,∴CD⊥AB,
∴∠OCE=30°,CE=DE,
∴OE=$\frac{1}{2}$OC=$\frac{1}{2}$OB=2,OC=4.
S阴影=$\frac{120°}{360°}×π×{4}^{2}$=$\frac{16π}{3}$.
故选D.
点评 本题考查了扇形的面积公式,证明△OEC≌△BED,得到S阴影=半圆-S扇形OCB是本题的关键.

练习册系列答案
相关题目
16.某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A、B两种产品共50件,生产A、B两种产品与所需原料情况如下表所示:
(1)该工厂生产A、B两种产品有哪几种方案?
(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?
| 原料 型号 | 甲种原料(千克) | 乙种原料(千克) |
| A产品(每件) | 9 | 3 |
| B产品(每件) | 4 | 10 |
(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?
20.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
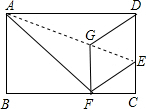 如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.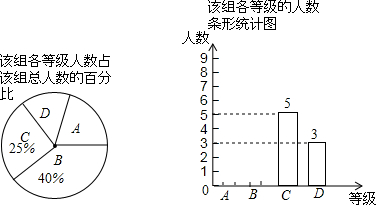
 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象经过点A. 如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°.
如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°.