题目内容
14．如图建立了一个由小正方形组成的网格（每个小正方形的边长为1）．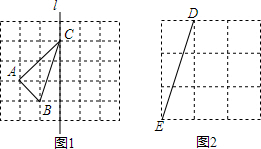
（1）在图1中，画出△ABC关于直线l对称的△A′B′C′；
（2）在图2中，点D，E为格点（小正方形的顶点），则线段DE=$\sqrt{10}$；若点F也是格点且使得△DEF是等腰三角形，标出所有的点F．
分析 （1）利用网格首先确定A、B、C三点关于直线l对称的对称点位置，再连接即可；
（2）利用勾股定理计算出DE的长，再根据AB的长度确定F点位置．
解答 
解：（1）如图所示：
（2）DE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
F点位置如图所示．
故答案为：$\sqrt{10}$．
点评 本题主要考查了等腰三角形的判定，作图--轴对称变换，以及勾股定理应用，关键是熟练掌握等腰三角形的判定定理．
练习册系列答案
阅读快车系列答案
相关题目
2．计算：72°22′+50°40′30″的结果是（ ）
| A． | 122°62′30″ | B． | 123°2′30″ | C． | 122°2′30″ | D． | 123°12′30″ |
9．在一个不透明的盒子中装有3个红球、2个黄球和1个绿球，这些球除了颜色外无其他差别．从中随机摸出一个小球，恰好是黄球的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
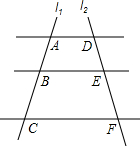如图，AD∥BE∥CF，直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F．已知AB=1，BC=3，DE=2，则EF的长为6．