题目内容
9.在一个不透明的盒子中装有3个红球、2个黄球和1个绿球,这些球除了颜色外无其他差别.从中随机摸出一个小球,恰好是黄球的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 直接根据概率公式求解.
解答 解:从中随机摸出一个小球,恰好是黄球的概率=$\frac{2}{3+2+1}$=$\frac{1}{3}$.
故选C.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
相关题目
17.下列说法中,正确的有( )
①$\frac{3xy}{5}$的系数是$\frac{3}{5}$;②-22ab2的次数是5;③多项式mn2+2mn-3n-1的次数是3;④a-b和$\frac{xy}{2}$都是整式.
①$\frac{3xy}{5}$的系数是$\frac{3}{5}$;②-22ab2的次数是5;③多项式mn2+2mn-3n-1的次数是3;④a-b和$\frac{xy}{2}$都是整式.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.-$\frac{1}{2}$的倒数与3的和是( )
| A. | -$\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -5 | D. | 1 |
19.如图,已知△ABC的六个元素,则下面甲、乙、丙、丁四个三角形中一定和△ABC全等的图形是( )

| A. | 甲、乙 | B. | 甲、丙 | C. | 甲、丁 | D. | 乙、丙 |
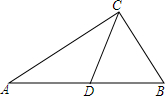 如图,已知△ABC中,∠C=90°,tanA=$\frac{1}{2}$,点D在边AB上,AD:DB=3:1,求cot∠DCB的值.
如图,已知△ABC中,∠C=90°,tanA=$\frac{1}{2}$,点D在边AB上,AD:DB=3:1,求cot∠DCB的值.