题目内容
3.在一个不透明的口袋中放入除颜色外其余都相同的6个红球和若干个绿球,小颖从中随机摸出一球,记下颜色后,放回,共试验60次,其中记有20个红球,估计袋中有绿球个数为( )| A. | 12 | B. | 18 | C. | 24 | D. | 40 |
分析 利用频率估计概率,可得到摸到红球的概率为$\frac{20}{60}$=$\frac{1}{3}$,设袋中有绿球x个数,于是根据概率公式得到$\frac{6}{x+6}$=$\frac{1}{3}$,然后解方程求出x即可.
解答 解:根据题意,小颖从中随机摸出一球,摸到红球的概率为$\frac{20}{60}$=$\frac{1}{3}$,
设袋中有绿球x个数,则$\frac{6}{x+6}$=$\frac{1}{3}$,解得x=12,
所以可估计袋中有绿球12个.
故选A.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.

练习册系列答案
相关题目
11. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
18.-$\frac{1}{2}$的倒数与3的和是( )
| A. | -$\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -5 | D. | 1 |
8.若(x-2)(x+3)=x2-ax+b,则a、b的值是( )
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=-1,b=-6 | D. | a=5,b=-6 |
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)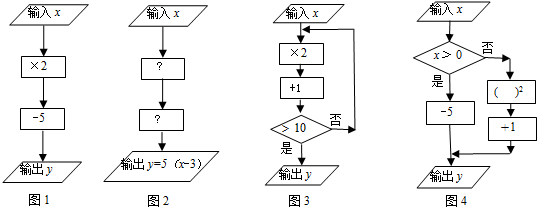
 ”内,应填-3;第二个运算框“
”内,应填-3;第二个运算框“ ”内,应填×5;
”内,应填×5;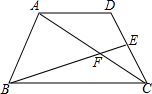 如图,梯形ABCD中,AD∥BC,BC=2AD,点E为边DC的中点,BE交AC于点F.求:
如图,梯形ABCD中,AD∥BC,BC=2AD,点E为边DC的中点,BE交AC于点F.求: