题目内容
20.为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌棕子,每盒进价是40元,超市规定每盒售价不得少于45元,根据以往销售经验发现:当售价定位每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒,当每盒定价多少元时,每天的销售利润可以达到8000元?分析 设每盒定价x元时,每天的销售利润可以达到8000元.根据“当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒”即可得出每天的销售量y(盒)与每盒售价x(元)之间的函数关系,由销售利润=销售数量×每盒的利润列出方程并解答.
解答 解:设每盒定价x元时,每天的销售利润可以达到8000元,
由题意得,(x-40)[700-20(x-45)]=8000,
解得x=60.
答:当每盒售价定为60元时,每天销售的利润是8000元.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列各数:5.9、-2$\frac{1}{3}$、-7、0、$\frac{12}{5}$、8中,正分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.独山县各学校开展了第二课堂的活动,在某校国学诗词组、篮球足球组、陶艺茶艺组三个活动组织中,若小斌和小宇两名同学每人随机选择其中一个活动参加,则小斌和小宇选到同一活动的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
12.一元二次方程(x-1)(x+2)=0的解是( )
| A. | 1 | B. | 1或-2 | C. | -1或2 | D. | -2 |

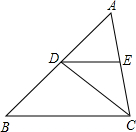 如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.
如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.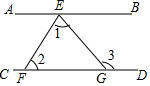 如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.
如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2. 已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.
已知,如图,AC⊥BC,BD⊥BC,AC>BC>BD.