题目内容
1.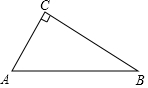 如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在Rt△ACB中,∠C=90°,∠A=60°,AB=8.点P是AB边上的一个动点,过点P作PD⊥AB交直角边于点D,设AP为x,△APD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 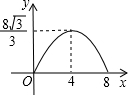 | B. | 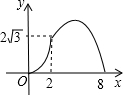 | C. | 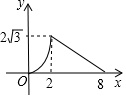 | D. |  |
分析 分点D在AC上和BC上两种情况进行讨论即可.
解答 解:∵∠C=90°,∠A=60°,AB=8,
∴AC=4,BC=4$\sqrt{3}$,
当点D在AC上时,y=$\frac{1}{2}$×AP×PD=$\frac{1}{2}$×x×$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2;
当点D在BC上时,如图所示,
∵AP=x,AB=8,
∴BP=8-x,又∠B=30°,
∴PD=$\frac{\sqrt{3}(8-x)}{3}$,
∴y=$\frac{1}{2}$AP•PD=$\frac{1}{2}$x•$\frac{\sqrt{3}(8-x)}{3}$=-$\frac{\sqrt{3}}{6}$x2+$\frac{4\sqrt{3}}{3}$x,
∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.
故选B.
点评 本题考查动点问题的函数图象,有一定难度,解题关键是注意点D在BC上这种情况.

练习册系列答案
相关题目
12.下列运算正确的是( )
| A. | (a-1)2=a2-1 | B. | (2a)2=2a2 | C. | a2•a3=a6 | D. | a•a2=a3 |
9.如图是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形,小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图,如图,A、B两点的距离为18米,则这种装置能够喷灌的草坪面积为( )(m2).

| A. | 36π | B. | 72π | C. | 144π | D. | 18π |
13. 如图,△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
 如图,△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )
如图,△ABC中,AB=AC,∠A=36°,BD,CE分别平分∠ABC和∠ACB,并交于点F,则图中全等三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
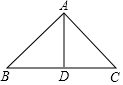 如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.
如图,△ABC的周长为20,且AB=AC,AD⊥BC于D,△ACD的周长为16,那么AD的长为6.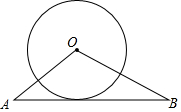 如图,已知在△OAB中,OA=OB=13,AB=24,⊙O的半径长为r=5,判断直线AB与⊙O的位置关系,并说明理由.
如图,已知在△OAB中,OA=OB=13,AB=24,⊙O的半径长为r=5,判断直线AB与⊙O的位置关系,并说明理由.