Question

5．如图，已知在⊙O中，AC是直径，CB是⊙O的切线，连接AB，AB与⊙O交于点D，连接OD，CD，E为BC上一点，连接DE，且CE=DE．
（1）若∠DCE=30°，OC=6，求$\widehat{CD}$的长度；
（2）求证：DE是⊙O的切线；
（3）试判断∠DCE与∠DOC之间的数量关系，并说明理由．

Answer 1

分析 （1）由于CB是⊙O的切线，根据∠DCE的度数可先求出∠DOE的角度，然后利用弧长公式即可求出答案
（2）连接OE，证明△ODE≌△OCE，然后利用对应角相等即可求出∠ODE=90°
（3）由于OD=OC，DE=CE，从而可知OE是CD的垂直平分线，从而可知∠DCE=∠COE

解答 解：（1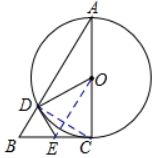）∵BC是⊙O的切线
∴∠ACB=90°，
∴∠ACD=∠ACB-∠DCE=60°，
∵OD=OC，
∴△COD是等边三角形，
∴∠COD=60°，
∴$\widehat{BC}$的长度为：$\frac{60°π×6}{180°}$=2π，
（2）连接OE，
在△ODE与△OCE中
$\left\{\begin{array}{l}{OD=OC}\\{OE=OE}\\{DE=CE}\end{array}\right.$
∴△ODE≌△OCE（SSS）
∴∠ODE=∠OCE=90°
∴DE是⊙O的切线
（3）由（2）可知∠DOE=∠COE
∵DE=CE
OD=OC
∴OE是CD的垂直平分线
∴∠DCE+∠OCD=∠OCD+∠COE=90°
∴∠DCE=∠COE
∴∠DCE=∠DOC

点评 本题考查圆的综合问题，涉及全等三角形的判定，切线的性质与判定，弧长公式，等边三角形的性质与判定，考查的知识较为综合，属于中等题型．