题目内容
17.解下列方程组:(1)$\left\{\begin{array}{l}{3x-y=7}\\{5x+2y=8}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{5}=1}\\{3(x+y)+2(x-3y)=15}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-y=7①}\\{5x+2y=8②}\end{array}\right.$,
①×2+②得:11x=22,
解得:x=2,
把x=2代入①得:6-y=7,
解得:y=-1,
则原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{5x+3y=15①}\\{5x-3y=15②}\end{array}\right.$,
①+②得:10x=30,即x=3,
①-②得:6y=0,即y=0,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
7.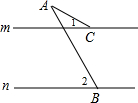 如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
 如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )
如图,直线m∥n,若∠1=25°,∠2=47°,则∠BAC的度数为( )| A. | 22° | B. | 25° | C. | 27° | D. | 30° |
12.下列各组数,能够作为直角三角形的三边长的是( )
| A. | 2,3,4 | B. | 4,5,7 | C. | 0.5,1.2,1.3 | D. | 12,36,39 |
9.下列语句中,不是命题的是( )
| A. | 经过一个点画一条直线 | B. | 两点之间,线段最短 | ||
| C. | 同角的余角相等 | D. | 对顶角不相等 |
7.下列调查适合普查的是( )
| A. | 调查2016年1月份市场上某品牌饮料的质量 | |
| B. | 了解甘肃电视台直播“两会”开幕式全国收视率情况 | |
| C. | 环保部门调查3月份长江某段水域的水质情况 | |
| D. | 为保证“神舟七号”飞船顺利升空,对其零部件进行调查 |
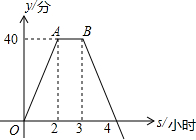 为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示
为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示