题目内容
12.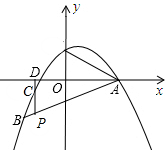 如图,抛物线y=-$\frac{1}{4}$x2+bx+c过点A(4,0),B(-4,-4).
如图,抛物线y=-$\frac{1}{4}$x2+bx+c过点A(4,0),B(-4,-4).(1)求抛物线的解析式;
(2)若点P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交抛物线及x轴于C、D两点.请问是否存在这样的点P,使PD=2CD?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法把问题转化为方程组解决.
(2)设P(m,$\frac{1}{2}$m-2),其中-4<m<4,则C(m,-$\frac{1}{4}$m2+$\frac{1}{2}$m+2),PD=2-$\frac{1}{2}$m,CD=|-$\frac{1}{4}$m2+$\frac{1}{2}$m+2|,分两种情形①当点C在x轴上方时,CD=-$\frac{1}{4}$m2+$\frac{1}{2}$m+2,由PD=2CD,得2-$\frac{1}{2}$m=2(-$\frac{1}{4}$m2+$\frac{1}{2}$m+2),②当点C在x轴下方时,CD=$\frac{1}{4}$m2-$\frac{1}{2}$m-2,由PD=2CD,列出方程即可解决问题.
解答 解:(1)由题意$\left\{\begin{array}{l}{-4+4b+c=0}\\{-4-4b+c=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=\frac{1}{2}}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2.
(2)∵A(4,0),B(-4,-4),
∴直线AB的解析式为y=$\frac{1}{2}$x-2,
设P(m,$\frac{1}{2}$m-2),其中-4<m<4,则C(m,-$\frac{1}{4}$m2+$\frac{1}{2}$m+2),PD=2-$\frac{1}{2}$m,CD=|-$\frac{1}{4}$m2+$\frac{1}{2}$m+2|,
①当点C在x轴上方时,CD=-$\frac{1}{4}$m2+$\frac{1}{2}$m+2,由PD=2CD,
得2-$\frac{1}{2}$m=2(-$\frac{1}{4}$m2+$\frac{1}{2}$m+2),解得m=-1或4(舍弃),
∴P(-1,-$\frac{5}{2}$).
②当点C在x轴下方时,CD=$\frac{1}{4}$m2-$\frac{1}{2}$m-2,由PD=2CD,得2-$\frac{1}{2}$m=2($\frac{1}{4}$m2-$\frac{1}{2}$m-2),解得m=-3或4(舍弃),
∴P(-3,-$\frac{7}{2}$),
综上所述,点P的坐标为(-1,-$\frac{5}{2}$)或(-3,-$\frac{7}{2}$).
点评 本题考查待定系数法确定函数解析式、二次函数的图象等知识,解题的关键是学会用方程的思想转化问题,学会用分类讨论的思想思考问题,属于中考常考题型.

| 购买苹果数 | 不超过30kg | 30kg以上 且不超过50kg | 50kg以上 |
| 每千克价格 | 4元 | 3.5元 | 3元 |
①乙班买苹果付了210元;
②乙班比甲班少付了45元;
③甲班第一次、第二次分别购买苹果多少千克?请写出计算过程.
(2)若甲班分两次购买苹果70kg(第二次多于第一次),并且第一次购买不少于10kg,如何购买最省钱?最省的钱是多少?请直接写出最省钱的购买方案.
| A. | x1=0,x2=2 | B. | x1=1,x2=2 | C. | x1=1,x2=-2 | D. | x1=0,x2=-2 |
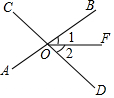 如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )
如图,直线AB、CD相交于点O,∠AOC=80°,∠2=45°,则∠1的度数为( )| A. | 70° | B. | 45° | C. | 35° | D. | 30° |
| A. | d≤$\sqrt{3}$cm | B. | d$<\sqrt{3}$cm | C. | d$≥\sqrt{3}$cm | D. | d$>\sqrt{3}$cm |
 如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )
如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( )| A. | 1cm2 | B. | 2cm2 | C. | 0.25cm2 | D. | 0.5cm2 |
 如图,在△ABC中,DB=DC,比较△ABD的面积与△ADC的面积的大小,则S△ABD=S△ADC(填写“<”,“=”,“>”)
如图,在△ABC中,DB=DC,比较△ABD的面积与△ADC的面积的大小,则S△ABD=S△ADC(填写“<”,“=”,“>”) 如图,△ABC是等边三角形,中线BD,CE相交于点O,则∠BOC=120°.
如图,△ABC是等边三角形,中线BD,CE相交于点O,则∠BOC=120°.